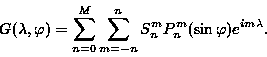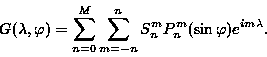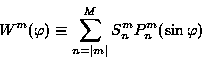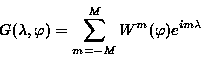戻る|進む
DCL:MATH2:SHTLIB : 球面調和関数
4.1 概要
これは, スペクトル(球面調和関数)変換を行なうサブルーチンパッケージであり,
球面調和関数展開の係数からグリッドデータ、およびその逆の変換を行なう.
このパッケージは, データ解析を念頭において設計されており,
等間隔グリッドデータを扱えるという特長がある.
また, スペクトルで与えられたデータの解析を念頭におき, 逆変換系のルーチ
ンを充実させている.
このパッケージの内部ではFFTLIBのサブルーチンを用いている.
切断波数M(三角切断)のスペクトル逆変換は, 以下のように表せる:
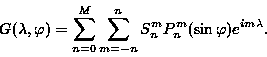 |
(4.1) |
または, ルジャンドル逆変換:
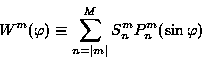 |
(4.2) |
を導入すると、
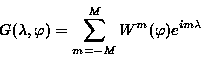 |
(4.3) |
と, ルジャンドル逆変換とフーリエ逆変換の積として表される.
ここに, λ:
経度, φ:
緯度である.
また,
Pmn(μ) は2に正規化されたルジャンドル陪関数で, 以下のように
定義される:
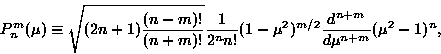 |
(4.4) |
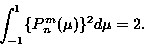 |
(4.5) |
また, スペクトル逆変換は以下のように表せる:
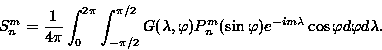 |
(4.6) |
逆変換の場合と同様に, フーリエ正変換を,
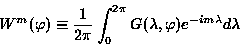 |
(4.7) |
と導入すると,
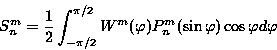 |
(4.8) |
と, フーリエ正変換とルジャンドル正変換の積として表される.
G(λ、φ)
が実数であるとすると, Smnおよび
Wm(φ)は以下の関係を満たしている必要がある:
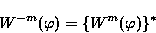 |
(4.9) |
ここに, {}*は複素共役を表す.
従って,
Wm(sinφ)
およびはm≧0の範囲だけを求めれば
良い. さらに, 上の制約から,
Wm(sinφ)およびS0nは実数である.
本ライブラリは,
スペクトルデータ(Smn) → 等間隔緯度円上のウエーブデータ(Wm(φj))
→ 等間隔格子点上のグリッドデータ( G(φj))
の逆変換を(1〜
3)式に基づいて行うルーチン群,
等間隔格子点上のグリッドデータ( G(φj)
) → 等間隔緯度円上のウエーブデータ(Wm(φj))
→ スペクトルデータ(Smn)
の正変換を(6〜8)式に基づいて行うルーチン群および
そして, その他の補助ルーチン群よりなっている.
ここに, 格子点の経度λi,
緯度φjは分割数I,Jによって
以下のように定められるものとする:
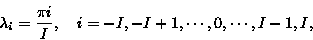 |
(4.11) |
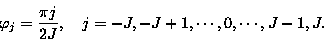
|
(4.12) |
戻る|進む
DCL:MATH2:SHTLIB : 球面調和関数