


: 大規模凝結
: 力学過程
: 力学過程
積雲パラメタリゼーションは
(Manabe et al., 1965)の対流調節スキームを用いている.
凝結した瞬間に水は系から取り除かれる. だから雨粒と雲は存在
しない.
湿潤対流調節が次の条件満足されるときに起こる.
- 2 つの隣接層間で, 大気が湿潤不安定になるとき,
つまり温度減率が湿潤断熱減率を越えたとき.
- 隣接 2 層の両方で飽和状態か過飽和状態になったとき.
調節の過程において,
隣接 2 層の温度と比湿とは即座に飽和状態と湿潤断熱減率との両方が
満たされる状態になる.
その過程において湿潤静的エネルギーは保存されなければならない.
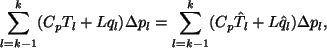 |
(13) |
ここで 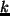 は鉛直方向に何層目かを表す指標である.
は鉛直方向に何層目かを表す指標である.
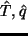 は調節前の値を,
一方
は調節前の値を,
一方 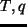 は調節後の値を表す.
は調節後の値を表す.
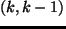 層の湿潤不安定条件は
層の湿潤不安定条件は
によって評価されている.
隣接 2 層の飽和状態は単純に
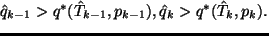 |
|
|
(15) |
によって表現されている.
調節された値 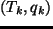 は次の式で決定される.
は次の式で決定される.
![\begin{displaymath}
\Delta T_{k}
= \frac{
(1 + \gamma_{k-1}) \Delta p_{k-1} ...
...k-1}
- (1 + \gamma_{k}) \Delta p_{k}]
} \raisebox{-5mm}{,}
\end{displaymath}](img73.gif) |
(20) |
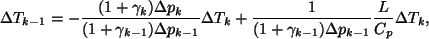 |
(21) |
ここで,
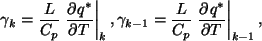 |
(22) |
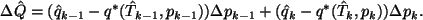 |
(23) |
ある気柱における降雨は次式によって計算される.
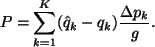 |
(24) |
これらの調節の手続きはすべての層において行なわれ
鉛直温度と水蒸気のプロファイルが収束するまで適用さえる.



: 大規模凝結
: 力学過程
: 力学過程
okuyama naonori
平成13年1月10日
![]() 層の湿潤不安定条件は
層の湿潤不安定条件は
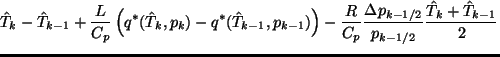
![]() は次の式で決定される.
は次の式で決定される.
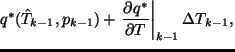
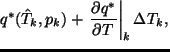
![\begin{displaymath}
\Delta T_{k}
= \frac{
(1 + \gamma_{k-1}) \Delta p_{k-1} ...
...k-1}
- (1 + \gamma_{k}) \Delta p_{k}]
} \raisebox{-5mm}{,}
\end{displaymath}](img73.gif)