|
乱流拡散係数 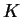 は Klemp and Wilhelmson (1978)
に従い乱流運動エネルギー
は Klemp and Wilhelmson (1978)
に従い乱流運動エネルギー
 から計算する.
熱に対する拡散係数は運動量に対する拡散係数に等しいとする.
地球大気中の積雲対流のシミュレーションにおいては,
Klemp and Wilhelmson (1978)
のパラメタリゼーションは空間格子スケール以下の乱流の表現に成功している.
本研究では火星大気中の乱流の表現に対してもこのパラメタリゼーションを
応用できると仮定する. から計算する.
熱に対する拡散係数は運動量に対する拡散係数に等しいとする.
地球大気中の積雲対流のシミュレーションにおいては,
Klemp and Wilhelmson (1978)
のパラメタリゼーションは空間格子スケール以下の乱流の表現に成功している.
本研究では火星大気中の乱流の表現に対してもこのパラメタリゼーションを
応用できると仮定する.
| |
|
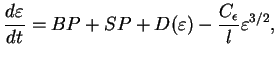 |
(A.9) |
| |
|
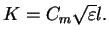 |
(A.10) |
ここで
 , ,  はそれぞれ浮力とシアーによる乱流エネルギー生成項で
はそれぞれ浮力とシアーによる乱流エネルギー生成項で
と表される.  は混合距離でモデルの鉛直格子間隔か高度のどちらか小さい方の値を与える.
は混合距離でモデルの鉛直格子間隔か高度のどちらか小さい方の値を与える.
(A.9)
右辺第 4 項は乱流エネルギーの散逸を表す. この項から散逸加熱  が計算される. が計算される.
 |
(A.13) |
|