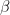 面上の2次元非発散系を考察する.支配方程式は次のように書きくだせる.
面上の2次元非発散系を考察する.支配方程式は次のように書きくだせる.ここではロスビー波をつかさどるもっとも単純な方程式を取り上げ,ロスビー波のイメージをつかむことにする.
系として 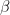 面上の2次元非発散系を考察する.支配方程式は次のように書きくだせる.
面上の2次元非発散系を考察する.支配方程式は次のように書きくだせる.
式1.1:
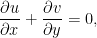
式1.2:
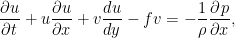
式1.3:
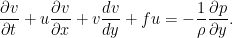
ただし 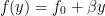 ,
, 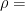 const. である*1.
const. である*1.
[*1] この導出についてはシリーズ `2次元非圧縮流体の支配方程式'を参照せよ
基本場が 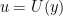 である流れに対する線型化された擾乱の方程式は,
である流れに対する線型化された擾乱の方程式は,
式1.4:
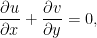
式1.5:
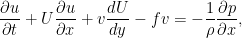
式1.6:
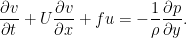
式1.1 より流れ関数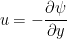 ,
,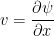 を導入することができる.式1.4 〜 式1.6より渦度方程式を作ると
を導入することができる.式1.4 〜 式1.6より渦度方程式を作ると
式1.7:
![\left( \DP{}{t} + U \DP{}{x} \right) \left( \DP[2]{}{x} + \DP[2]{}{y} \right) \psi + \left(\beta - \DD[2]{U}{y}\right) \DP{\psi}{x} = 0.](images/_review_math/_gen_1093c179e967fd3ddbba4a15d4396dd1718933f05d4a945100c21fccfeffcbf9.png)
この方程式は, もともとのポテンシャル渦度保存則において,基本場のポテンシャル渦度を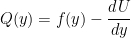 ,擾乱のポテンシャル渦度は
,擾乱のポテンシャル渦度は 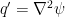 ,速度
,速度 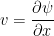 とした場合に相当する.
とした場合に相当する.
特に 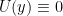 のとき, 線型化された方程式は
のとき, 線型化された方程式は
式1.8:
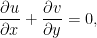
式1.9:
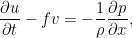
式1.10:
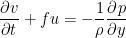
また, 式1.7 は次のようになる.
式1.11:
![\DP{}{t} \left( \DP[2]{}{x} + \DP[2]{}{y} \right)\psi + \beta \DP{\psi}{x} = 0.](images/_review_math/_gen_4f17cbedc818c7e4f4b570dd20c75af54277ca257c7074ea5e0a53f4870dc26c.png)
分散関係式をもとめるために 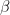 を一定とし,解として平面波の形
を一定とし,解として平面波の形 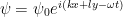 を支配方程式に代入し整理すると,
を支配方程式に代入し整理すると,
式1.12:
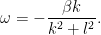
これが 2 次元非発散ロスビー波の分散関係である.
式1.13:
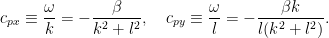
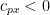 より, 位相は常に
より, 位相は常に  軸負方向(西向き)に進む.
軸負方向(西向き)に進む.
式1.14:
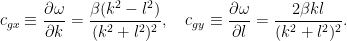
 の波束は
の波束は  軸正方向(東向き),
軸正方向(東向き), の波束は
の波束は  軸負方向(西向き)にエネルギーを伝播する.
軸負方向(西向き)にエネルギーを伝播する.
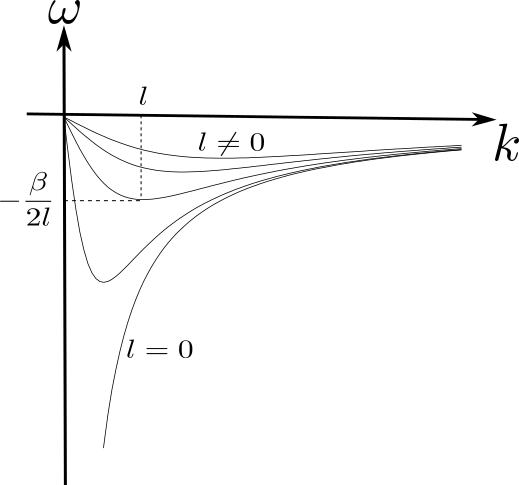
図1.1: 2次元非発散ロスビー波の分散関係(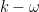 面)
面)
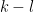 面での分散関係の表現
面での分散関係の表現式1.12を変型することにより
式1.15:
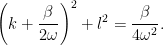
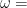 const.である
const.である 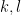 を
を 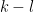 面で表すと円になる(図1.2).また群速度は
面で表すと円になる(図1.2).また群速度は 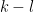 面での
面での 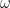 の gradient(
の gradient(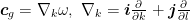 )であるから,その向きは式1.15の円の中心から円周上の点に向かう向きとなる.
)であるから,その向きは式1.15の円の中心から円周上の点に向かう向きとなる.

図1.2: ロスビー波の分散関係 (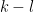 面)
面)
2 次元 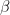 面内に初期擾乱を与えたときの時間変化の計算例を図1.3に示す.与えられた擾乱がロスビー波として伝播し, 分散していく.図1.3
面内に初期擾乱を与えたときの時間変化の計算例を図1.3に示す.与えられた擾乱がロスビー波として伝播し, 分散していく.図1.3 において下図のような位相と群速度の関係が見られる.
において下図のような位相と群速度の関係が見られる.
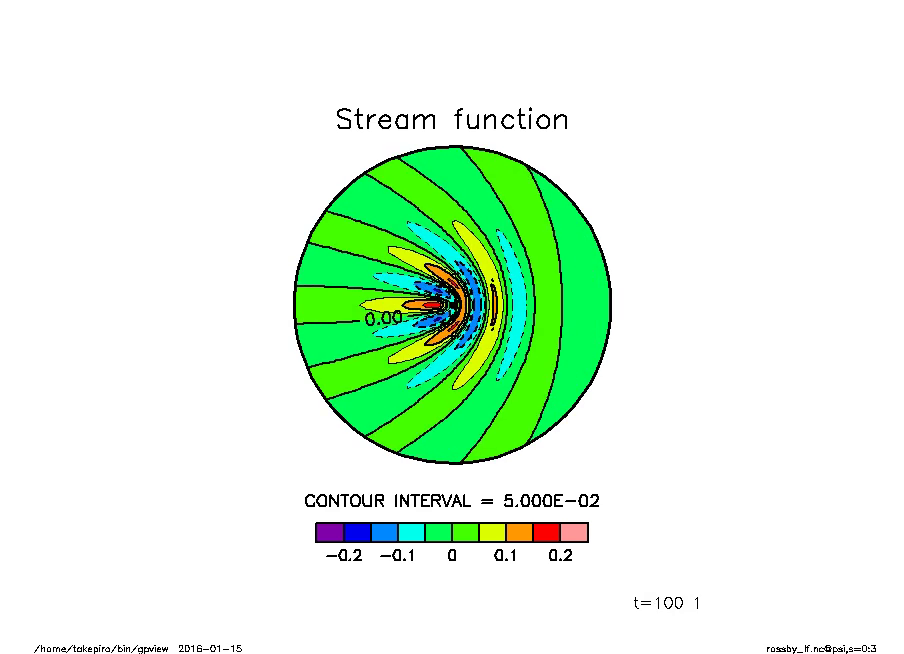
図1.3: 初期点擾乱を与えたときの流線の時間変化.トーンの塗り方は全て同じだが, 振幅の大きいところは塗っていない.