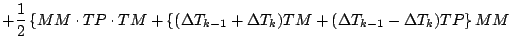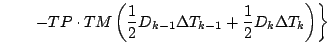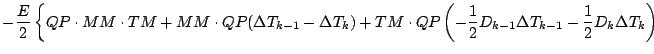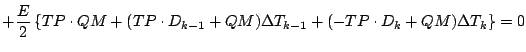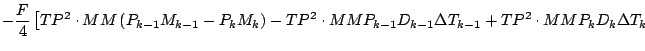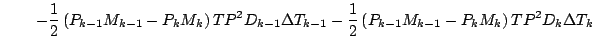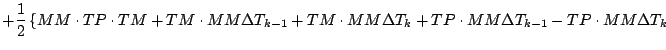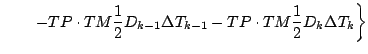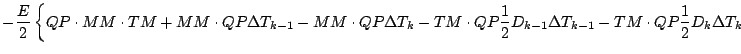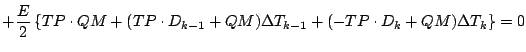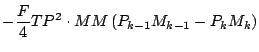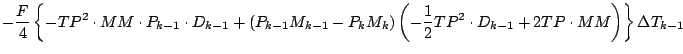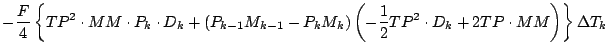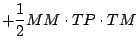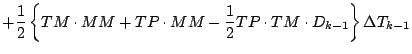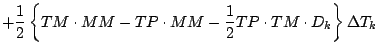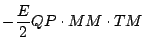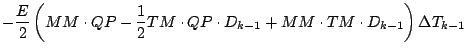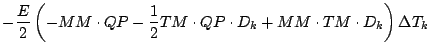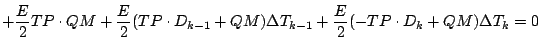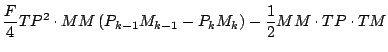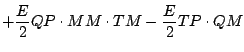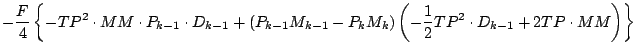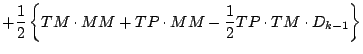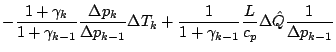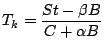

: 5 放射
: DCAPM4 第1部 数理モデル化
: 3 支配方程式・力学過程
3 33
3
33
3 33
33
大気大循環モデルにおいては
積雲を様に表現するだけの分解能を持たないので,
雲の発生する条件
並びに雲が大気大循環に与える影響については
何らかの方法で評価せざるを得ない.
雲が発生する条件および
雲が大気大循環に与える影響のうちの
熱・運動量輸送効果については4,
大規模場の速度や熱力学的諸量から評価することが多い.
この評価方法は一般に積雲パラメタリゼーションと呼ばれ,
特に以下の型のものが良く用いられる.
- 湿潤対流調節
- クオスキーム
- 浅い積雲5
- 荒川シューバートスキーム6
また, そもそも大気が過飽和状態にあれば降水が起こる.
これを大規模凝結という.
以下では各種パラメタリゼーション並びに大規模凝結について解説する.
6 66
66
連続した 2 つのレベルの間の層において, 次の条件が
満たされる時調節を行う.
- 温度減率が湿潤断熱減率よりも大きい
- 飽和もしくは過飽和.
上記の条件 (1) に関して,
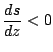 |
|
|
(31) |
の条件を, 「水蒸気が少ない」という近似をふんだんに
用いて書きかえると
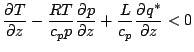 |
|
|
(32) |
となる.
上記の条件 (2) に関しては, そのまま使う.
これらを用いて温度と比湿を調節するのが dcpam のデフォルトの
湿潤対流調節スキームである.
以下, スキームの定式化の説明を行う.
(差分法と混ざった話になってしまっているので, あとでちゃんと整理が
必要だとおもう).
比湿と温度を,
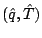 から
から 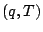 へ
調節するものとする.
へ
調節するものとする.
条件式は以下の通りである.
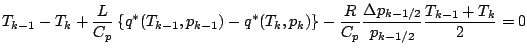 |
|
|
(35) |
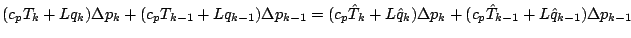 |
|
|
(36) |
解は以下のようになる(で, 良いんだっけかな?)
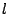 が一定の場合,
が一定の場合,
全部 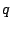 を使って書き換えた.
更に変形すると
を使って書き換えた.
更に変形すると
これより, 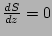 となる条件は
となる条件は
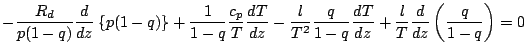 |
|
|
(53) |
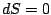 の式をどのような形にするのが best なのかは
よくわからない.
とりあえず, 扱いが容易かなと思った分母を全部払った
形にしてみる.
の式をどのような形にするのが best なのかは
よくわからない.
とりあえず, 扱いが容易かなと思った分母を全部払った
形にしてみる.
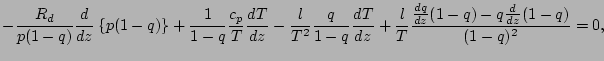 |
|
|
|
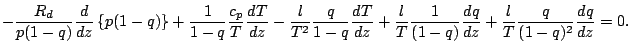 |
|
|
(54) |
この式の両辺に 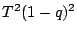 をかける.
をかける.
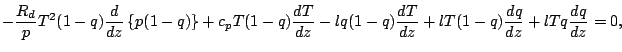 |
|
|
|
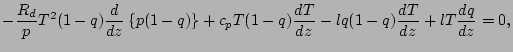 |
|
|
(55) |
更に 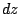 をかければ
をかければ
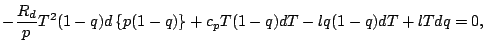 |
|
|
(56) |
近似をせずに, 分母を払った形の式をそのまま離散化する.
| |
|
![$\displaystyle - \frac{R_d}{p_{k-1/2}} T_{k-1/2}^2 (1-q_{k-1/2})
\left[ p_{k-1} ...
...k-1}) - p_{k} (1-q_{k}) \right]
+ c_p (1-q_{k-1/2}) T_{k-1/2}
(T_{k-1} - T_{k})$](img164.png) |
|
| |
|
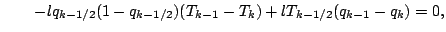 |
(57) |
ここで,
とすると(これ, 本当は良くないのだろう. 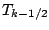 については
Arakawa and Suarez (1983) の正しい補間式を使うべきなような気がする.
しかし, agcm5 時代に, サブルーチンの引数を変えるのが嫌だったので
こうしている. dcpam ではサブルーチン内で
については
Arakawa and Suarez (1983) の正しい補間式を使うべきなような気がする.
しかし, agcm5 時代に, サブルーチンの引数を変えるのが嫌だったので
こうしている. dcpam ではサブルーチン内で 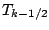 を作る
のでも良いかもしれない),
を作る
のでも良いかもしれない),
潜熱が大文字になっちゃった...
最初から 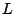 にしておくべき.
にしておくべき.
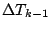 などを使って書き換える.
などを使って書き換える.
ここで, 以下の変数達を導入する.
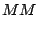 |
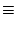 |
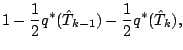 |
(62) |
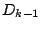 |
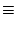 |
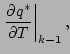 |
(63) |
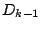 |
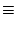 |
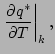 |
(64) |
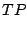 |
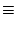 |
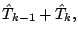 |
(65) |
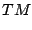 |
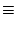 |
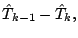 |
(66) |
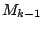 |
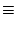 |
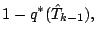 |
(67) |
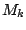 |
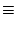 |
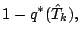 |
(68) |
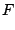 |
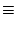 |
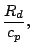 |
(69) |
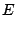 |
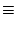 |
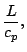 |
(70) |
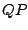 |
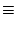 |
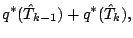 |
(71) |
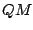 |
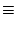 |
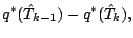 |
(72) |
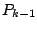 |
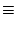 |
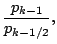 |
(73) |
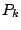 |
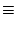 |
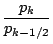 |
(74) |
これらの記号を用いて, 先程の式を書き換えると以下のように
なる.
この式をまともに解くことは大変なので, やむをえず近似する.
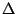 が 2 つ以上かかった項を無視することにする.
おそらく「1 次近似」と言って良いのだろう, とは
思っているが, この近似の妥当性に関して現段階ではまったく
検討していない.
が 2 つ以上かかった項を無視することにする.
おそらく「1 次近似」と言って良いのだろう, とは
思っているが, この近似の妥当性に関して現段階ではまったく
検討していない.
式を展開しつつ「2 次以上の項」を順次無視していくと, 以下のようになる.
更に第 1 項を展開する.
この式を
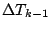 の項と
の項と 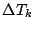 の項に
まとめていく. まずばらす.
の項に
まとめていく. まずばらす.
ついで, まとめる.
ここで, 以下のように変数をまとめる (前の 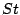 とはちゃんと対応
しているんだろうね???).
とはちゃんと対応
しているんだろうね???).
これより,
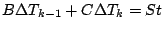 |
|
|
(84) |
となる.
ここで, 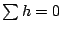 より得られる
より得られる
を代入すると
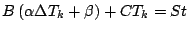 |
|
|
(87) |
これを, 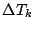 について解けば
について解けば
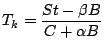 |
|
|
(88) |
- ...
熱・運動量輸送効果については4
-
- ... 浅い積雲5
-
dennou モデルには Tiedtke による, 係数を増やす形のもの
がある.
- ... 荒川シューバートスキーム6
-
dcpamには現在存在しない.


: 5 放射
: DCAPM4 第1部 数理モデル化
: 3 支配方程式・力学過程
Yasuhiro MORIKAWA
平成19年7月31日
![]() 66
66
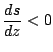
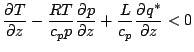
![]() から
から ![]() へ
調節するものとする.
へ
調節するものとする.
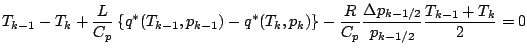
![]() ,
,
![]() が求められたとすると,
「飽和するべし」という条件から,
が求められたとすると,
「飽和するべし」という条件から,
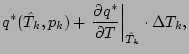
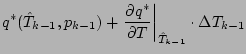
![]() がわかったとすると,
がわかったとすると,
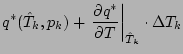
![]() より
より
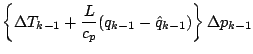
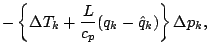
![$\displaystyle \left[ \Delta T_{k-1}
+ \frac{L}{c_p}
\left\{ q^{*} (\hat{T}_{k-1...
...ight\vert _{k-1}
\Delta T_{k-1}
- \hat{q}_{k-1}
\right\}
\right] \Delta p_{k-1}$](img110.png)
![$\displaystyle = - \left[ \Delta T_{k}
+ \frac{L}{c_p}
\left\{ q^{*} (T_{k})
+ \...
...}{T} \right\vert _{k}
\Delta T_{k}
- \hat{q}_{k}
\right\}
\right] \Delta p_{k},$](img111.png)
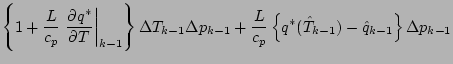
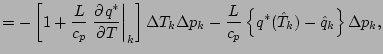
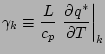
![$\displaystyle =
- \left( 1
+ \gamma_{k}
\right) \Delta T_{k} \Delta p_{k}
+ \fr...
...{k-1}
+ \left\{ \hat{q}_{k} - q^{*} (\hat{T}_{k}) \right\}
\Delta p_{k}
\right]$](img116.png)
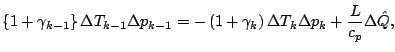
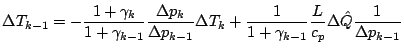
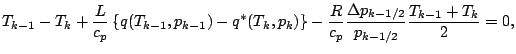
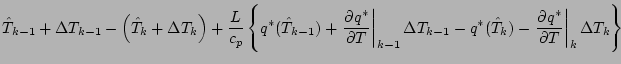
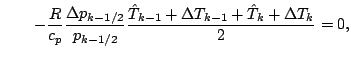
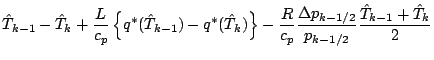
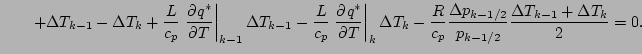
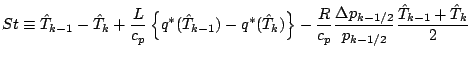
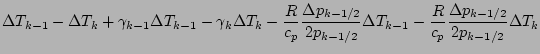
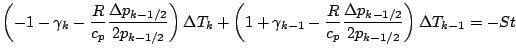
![]() の表式を代入する.
の表式を代入する.
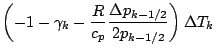
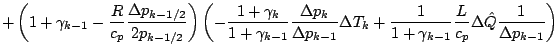
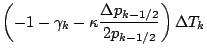
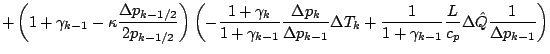
![$\displaystyle \left[
\left( - 1 - \gamma_{k} \right)
- \kappa
\frac{\Delta p_{k...
... \gamma_{k-1}}
\frac{\Delta p_{k}}{\Delta p_{k-1}}
\right)
\right]
\Delta T_{k}$](img141.png)
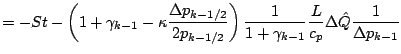
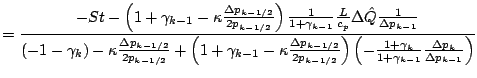
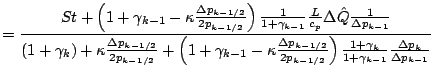
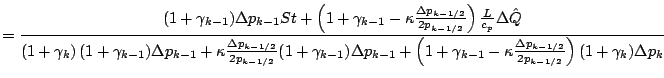
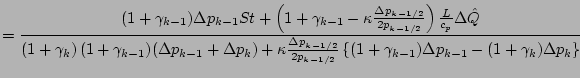
![]() が一定の場合,
が一定の場合,
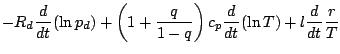
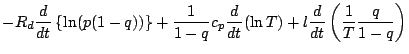
![$\displaystyle - R_d \frac{1}{p (1-q)} \DD{}{t} \left\{ p (1-q) \right\}
+ \frac...
...T}{t} \frac{q}{1-q}
+ \frac{1}{T} \DD{}{t} \left( \frac{q}{1-q} \right)
\right]$](img153.png)
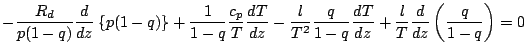
![]() の式をどのような形にするのが best なのかは
よくわからない.
とりあえず, 扱いが容易かなと思った分母を全部払った
形にしてみる.
の式をどのような形にするのが best なのかは
よくわからない.
とりあえず, 扱いが容易かなと思った分母を全部払った
形にしてみる.
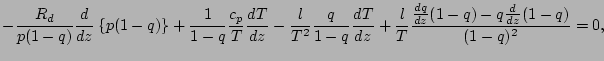
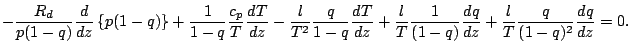
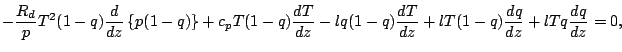
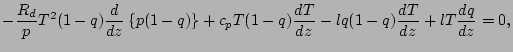
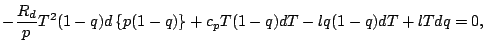
![$\displaystyle - \frac{R_d}{p_{k-1/2}} T_{k-1/2}^2 (1-q_{k-1/2})
\left[ p_{k-1} ...
...k-1}) - p_{k} (1-q_{k}) \right]
+ c_p (1-q_{k-1/2}) T_{k-1/2}
(T_{k-1} - T_{k})$](img164.png)
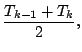
![$\displaystyle - \frac{R_d}{p_{k-1/2}}
\left( \frac{T_{k-1} + T_{k}}{2} \right)^...
..._{k-1} + q_{k}}{2} \right)
\left[ p_{k-1} (1-q_{k-1}) - p_{k} (1-q_{k}) \right]$](img171.png)
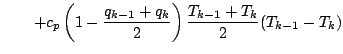
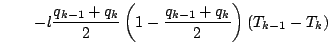
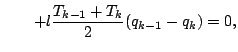
![$\displaystyle - \frac{R_d}{c_p}
\left( \frac{T_{k-1} + T_{k}}{2} \right)^2
\lef...
...rac{p_{k-1}}{p_{k-1/2}} (1-q_{k-1})
- \frac{p_{k}}{p_{k-1/2}} (1-q_{k})
\right]$](img175.png)
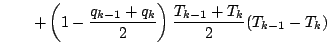
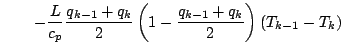
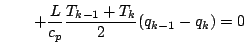
![]() などを使って書き換える.
などを使って書き換える.
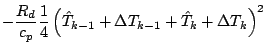
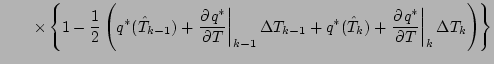
![$\displaystyle \qquad
\times
\left[ \frac{p_{k-1}}{p_{k-1/2}}
\left( 1 - q^{*} (...
...at{T}_{k}) - \left. \DP{q^{*}}{T} \right\vert _{k} \Delta T_{k}
\right)
\right]$](img182.png)
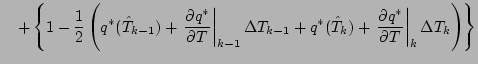
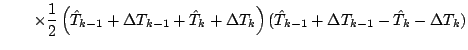
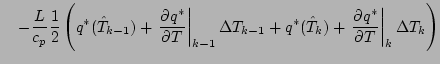
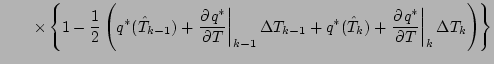
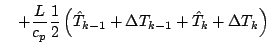
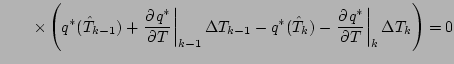
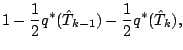
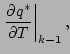
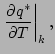
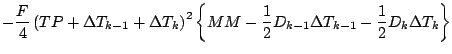
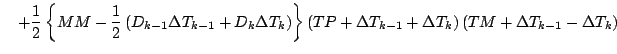
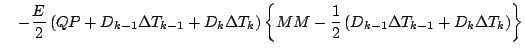
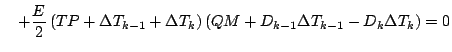
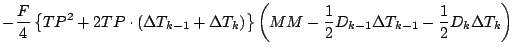
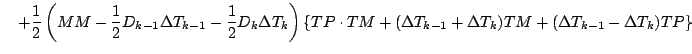
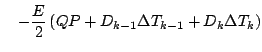
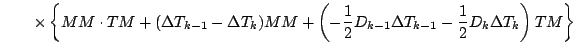
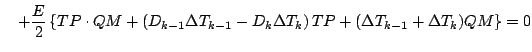
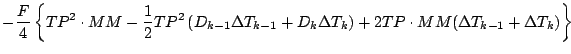
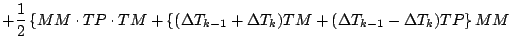
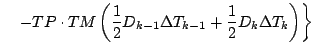
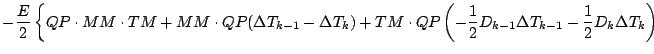
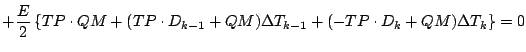
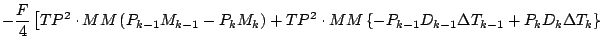
![$\displaystyle \qquad \left.
+ \left( P_{k-1} M_{k-1} - P_{k} M_{k} \right)
\lef...
... T_{k}
\right)
+ 2 TP \cdot MM (\Delta T_{k-1} + \Delta T_{k})
\right\}
\right]$](img235.png)