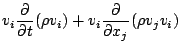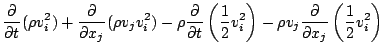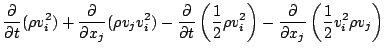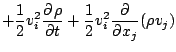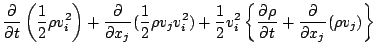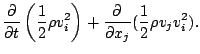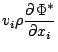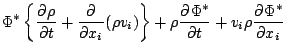

: 5 地球定数
: DCAPM2 第1部 数理モデル化
: 3 支配方程式・力学過程
支配方程式系の導出
3 33
3
33
3 33
33
全大気は, ともに理想気体である乾燥空気および水蒸気から成る混合大気とす
る. 雲水量は無視する. また, 水蒸気量が全大気に占める割合は小さいと仮定
し, 全大気の定圧比熱を乾燥大気の値で近似する.
水蒸気量の保存については, 凝結および蒸発による生成消滅を考慮する. しか
し, この量が全大気に与える効果は小さいとし, 全大気の質量保存則, 運動エ
ネルギー保存則, 全エネルギー保存則に影響を及ぼさないとする.
重力加速度は地球中心に向いていると仮定する. また, 運動の水平スケールが
鉛直スケールよりもかなり大きい運動を想定し, 静力学平衡近似を行なう. さ
らに, 運動は地球表面付近に限られることを仮定して近似を行なう.
3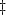 33
3
33
3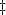 33
33
方程式系は 6 本の予報方程式と 1 本の診断方程式からなる. 予報方程式は,
全質量の連続の式, 水蒸気量の式, 運動方程式(3 �$B@.J,), 熱力学の式からなる.
これらは, それぞれ, 全質量保存則, 水蒸気量の保存則, 全質量に関する運動
量保存則, 全質量に関する全エネルギー保存則から導出する. 診断方程式には,
理想気体の状態方程式を用いる.
4
!!注意: この Appendix 中では導出の都合上, 乾燥空気の気体定数を 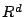 定圧比熱を
定圧比熱を 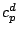 とし, 全大気の気体定数を
とし, 全大気の気体定数を 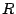 とおいた. しかし, 本文
中では, 乾燥空気の気体定数を
とおいた. しかし, 本文
中では, 乾燥空気の気体定数を 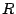 , 定圧比熱を
, 定圧比熱を 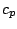 と表記している.
と表記している.
乾燥空気, 水蒸気の状態方程式はそれぞれ
である. ここで 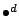 ,
, 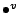 はそれぞれ乾燥空気および水
蒸気に関する量であることを示す. したがって, 全圧
はそれぞれ乾燥空気および水
蒸気に関する量であることを示す. したがって, 全圧 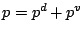 は,
は,
となる. ここで, 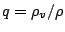 は比湿, であり,
は比湿, であり,
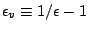 ,
,
 である. したがって,
全大気の状態方程式は,
である. したがって,
全大気の状態方程式は,
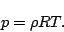 |
(35) |
ただし,
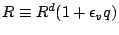 である. あるいは, 仮温度
である. あるいは, 仮温度
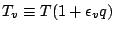 を用いれば,
を用いれば,
 |
(36) |
全大気の質量保存則は, 水蒸気の生成消滅を無視すれば,
5
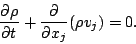 |
(37) |
あるいは, ラグランジュ形式で記述すれば,
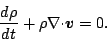 |
(38) |
水蒸気密度 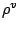 に対する質量保存則は, 単位時間単位体積あたりの生成
消滅量を
に対する質量保存則は, 単位時間単位体積あたりの生成
消滅量を 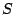 とすれば,
とすれば,
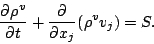 |
(39) |
比湿 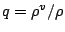 に関する式は, 原理的には式(
に関する式は, 原理的には式(![[*]](crossref.png) ) と式(A.9) から得ることができる. しかし,
今の場合, 式(A.7)で水蒸気の生成消滅を無視したので,
正しくは得られない. そこで比湿の生成消滅に関する項を改めて
) と式(A.9) から得ることができる. しかし,
今の場合, 式(A.7)で水蒸気の生成消滅を無視したので,
正しくは得られない. そこで比湿の生成消滅に関する項を改めて 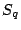 と定
義する.
と定
義する.
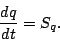 |
(40) |
運動量保存則は, 水蒸気の生成消滅にともなう運動量変化を無視すれば次のよ
うに書ける.
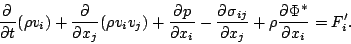 |
(41) |
ここで, 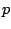 は圧力,
は圧力, 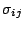 は粘性応力テンソル,
は粘性応力テンソル,  は地球
の引力によるポテンシャル
6 ,
は地球
の引力によるポテンシャル
6 , 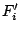 はその他の外力項である. あるいは連続の式
を用いてラグランジュ形式で記述すると
はその他の外力項である. あるいは連続の式
を用いてラグランジュ形式で記述すると
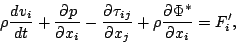 |
(42) |
となる. ここで, 粘性項と外力項を 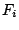 とおき, さらにベクトル表示する
とおき, さらにベクトル表示する
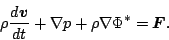 |
(43) |
単位質量あたりの全エネルギーは, 運動エネルギー 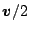 と内部エ
ネルギー
と内部エ
ネルギー 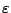 およぼポテンシャルエネルギー
およぼポテンシャルエネルギー  の和で表
現される. この時間変化率の式は, 水蒸気の生成消滅による影響を無視すれば,
の和で表
現される. この時間変化率の式は, 水蒸気の生成消滅による影響を無視すれば,
![\begin{displaymath}
\DP{}{t}
\left[ \rho
\left( \frac{1}{2} \Dvect{v}^2
+...
...v_j
+ p v_j - \sigma_{ij}v_i
\right]
= \rho Q + F'_i v_i,
\end{displaymath}](img120.png) |
(44) |
である. ここで, 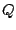 は外界からの加熱率である. 一方, 運動エネルギーとポ
テンシャルエネルギーの和の保存式は, 運動量保存式 (
は外界からの加熱率である. 一方, 運動エネルギーとポ
テンシャルエネルギーの和の保存式は, 運動量保存式 (![[*]](crossref.png) ) に
) に 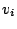 をかけ連続の式を用いて変形することで得られる. 変形の際に
は
をかけ連続の式を用いて変形することで得られる. 変形の際に
は
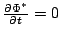 であるとしている.
7
であるとしている.
7
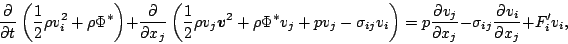 |
(45) |
となる. 式 (A.14) から式 (![[*]](crossref.png) ) を引き去ると, 次のように内部エネルギーの式が
得られる.
) を引き去ると, 次のように内部エネルギーの式が
得られる.
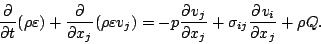 |
(46) |
連続の式を用いてラグランジュ形式に書き直せば
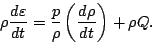 |
(47) |
ここで, 外界からの加熱の項と粘性による加熱の項をまとめて 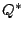 とおい
た.
とおい
た.
内部エネルギーを温度を用いて表現すると
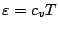 であ
る. さらに状態方程式 (A.5) を用いて式 (A.17)
を変形する.
であ
る. さらに状態方程式 (A.5) を用いて式 (A.17)
を変形する. 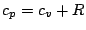 であることに注意すれば
であることに注意すれば
 |
(48) |
となる. ここで, 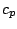 を乾燥空気の定圧比熱
を乾燥空気の定圧比熱 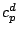 (定数) で近似すると
8次の熱力学の式を得る.
(定数) で近似すると
8次の熱力学の式を得る.
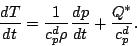 |
(49) |
8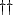 88
8
88
8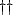 88
88
方程式系を, 一定の自転角速度
 で回転する回転系に変換す
る.
で回転する回転系に変換す
る.
慣性系における時間微分を添字 a で, 回転系を添字 r で表現する. このとき,
任意のスカラー 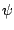 に対して,
に対して,
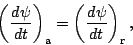 |
(50) |
が成りたつ.
9
任意のベクトル  に対する慣性系および回転系での微分は次の関
係をもつ.
に対する慣性系および回転系での微分は次の関
係をもつ.
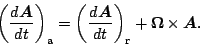 |
(51) |
(証明) 任意のベクトル  を, 慣性系では
を, 慣性系では
| |
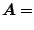 |
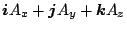 |
(52) |
と表し, 回転系では
| |
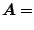 |
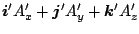 |
(53) |
と表す.
時間微分をとると
(証明終り)
ここで
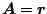 (
( 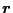 は位置ベクトル ) とおけば慣
性系での速度
は位置ベクトル ) とおけば慣
性系での速度
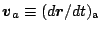 (これまでの
(これまでの
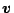 ) は回転系での速度
) は回転系での速度
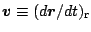 を用いて次のように表すことができる.
を用いて次のように表すことができる.
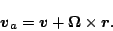 |
(55) |
さらに, 式(A.21) で
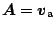 とお
けば, 速度の時間微分項は
とお
けば, 速度の時間微分項は
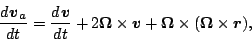 |
(56) |
と変換できる.
変換の式 (A.26) を用いて運動方程式を回転系で記述する.
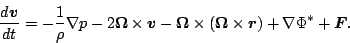 |
(57) |
ここで, 重力加速度
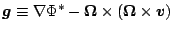 を定義すれば, 運動方程式は
を定義すれば, 運動方程式は
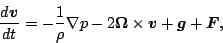 |
(58) |
となる.
連続の式および熱力学の式においては, ラグランジュ微分が作用している密度
および温度は座標変換に無関係なスカラーであるため, その時間微分の形は変
わらない. 連続の式は, 速度場の発散を含むが, これは座標変換によっても値
は変わらない. したがって, これらの式は形を変えない.
10
10
1010
10
1010
一般の直交曲線座標
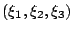 において, スカラー
において, スカラー
 およびベクトル
およびベクトル
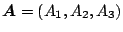 は次のように表現
される. なお,
は次のように表現
される. なお, 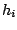 は各軸方向の規模因子であり, 各軸方向の基底ベクトル
は
は各軸方向の規模因子であり, 各軸方向の基底ベクトル
は 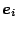 とする.
とする.
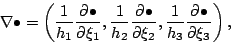 |
(59) |
![\begin{displaymath}
\Ddiv \Dvect{A}
= \frac{1}{h_1 h_2 h_3}
\left[ \DP{}{\x...
...\xi_2} ( h_1 h_3 A_2)
+ \DP{}{\xi_3} ( h_1 h_2 A_3)
\right],
\end{displaymath}](img175.png) |
(60) |
![\begin{displaymath}
\nabla^2 \bullet
= \frac{1}{h_1 h_2 h_3}
\left[ \DP{}{\...
...eft( \frac{h_1 h_2}{h_3} \DP{\bullet}{\xi_3} \right)
\right],
\end{displaymath}](img176.png) |
(61) |
![\begin{displaymath}
\Drot \Dvect{A}
= \left( \frac{1}{h_2 h_3}
\left[ \DP{(h_...
...DP{(h_2 A_2)}{\xi_1} - \DP{(h_1 A_1)}{\xi_2} \right]
\right),
\end{displaymath}](img177.png) |
(62) |
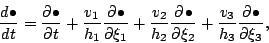 |
(63) |
![\begin{displaymath}
\DD{\Dvect{v}}{t}
= \sum^3_{k=1} \Dvect{e}_k
\left[ \DP{v...
...{v_k}{h_k} \frac{1}{h_j} \DP{h_k}{\xi_j} \right) v_j
\right].
\end{displaymath}](img179.png) |
(64) |
重力加速度 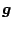 が地球中心を向いているとみなして, 方程式系を球
座標
が地球中心を向いているとみなして, 方程式系を球
座標
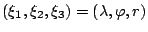 に変換する. 回転
系に固定した直交直線座標
に変換する. 回転
系に固定した直交直線座標
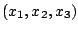 との関係は
との関係は
である. ここで, 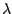 は緯度,
は緯度, 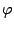 は経度,
は経度, 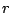 は鉛直座標であ
る. また, 基底ベクトルを
は鉛直座標であ
る. また, 基底ベクトルを
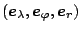 , 速度ベクトルを
, 速度ベクトルを 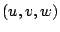 で表す.
で表す.
各方向の規模因子( scale factor )は
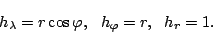 |
(68) |
したがって, スカラー  およびベクトル
およびベクトル
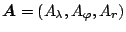 に関する微分表現は次のよう
になる.
に関する微分表現は次のよう
になる.
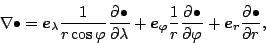 |
(69) |
![\begin{displaymath}
\Ddiv \Dvect{A}
= \frac{1}{r^2 \cos \varphi}
\left[ r \...
...hi A_{\varphi})
+ \cos \varphi \DP{}{r} ( r^2 A_r )
\right],
\end{displaymath}](img195.png) |
(70) |
![\begin{displaymath}
\nabla^2 \bullet
= \frac{1}{r^2 \cos \varphi}
\left[ \D...
...}{r} \left( r^2 \cos \varphi \DP{\bullet}{r} \right)
\right],
\end{displaymath}](img196.png) |
(71) |
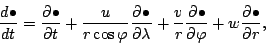 |
(73) |
自転角速度ベクトルの表現は次のようになる.
したがって, 運動方程式は
連続の式は
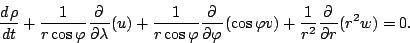 |
(80) |
熱力学の式は
 |
(81) |
状態方程式は
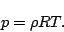 |
(82) |
水蒸気の式は
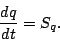 |
(83) |
ここで,
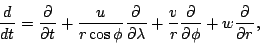 |
(84) |
である.
10
1010
10
1010
10
1010
鉛直方向の運動方程式に対し, 静力学平衡近似を行なう.
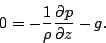 |
(85) |
このとき, 運動エネルギーの保存則を考慮して, 水平方向の運動方程式に対し
ても近似を施す. 運動エネルギーの式は, 運動方程室�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就甍弘鹸繞抗絛絨後縺⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩�砲修譴召�  をかけることで得られる.
をかけることで得られる.
コリオリの力およびメトリック項は同じ番号のもの同士で打ち消しあって, 運
動エネルギーの時間変化に寄与しないことがわかる.
11したがって, 静力学平衡近似の際に鉛直成分の式から落とした項(2),(4),(5)
�$B$KBP1~$7$??eJ?@.J,$N<0$N9`$b
ここで, 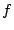 はコリオリパラメータ
はコリオリパラメータ
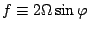 であ
る.
であ
る.
大気の層が地球半径に比べて薄いことを仮定し, 方程式中の 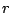 を, 代表的
な地球半径
を, 代表的
な地球半径 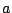 でおきかえる. また,
でおきかえる. また, 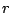 による微分はすべて海抜高度
による微分はすべて海抜高度 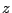 による微分でおきかえる. このとき基礎方程式は次のようになる.
による微分でおきかえる. このとき基礎方程式は次のようになる.
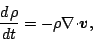 |
(89) |
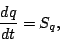 |
(90) |
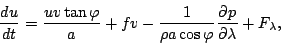 |
(91) |
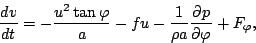 |
(92) |
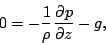 |
(93) |
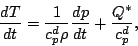 |
(94) |
 |
(95) |
ここで,
 |
(96) |
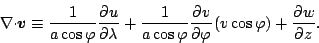 |
(97) |
11
1111
11
1111
静力学平衡のもとでは, 気圧 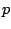 は鉛直座標
は鉛直座標 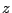 に対し単調減少する関数で
ある. そこで, 鉛直座標を
に対し単調減少する関数で
ある. そこで, 鉛直座標を 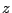 から, 地表面気圧
から, 地表面気圧 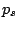 で規格化した気圧座
標,
で規格化した気圧座
標,
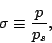 |
(98) |
に変換する.  と
と 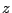 の関係は, 静力学平衡の式を変形して得られる.
の関係は, 静力学平衡の式を変形して得られる.
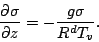 |
(99) |
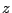 - 座標から
- 座標から  - 座標への変換公式を示す.
- 座標への変換公式を示す.
鉛直微分
水平微分
時間微分
ラグランジュ微分はこれらを用いて,
ここで,  -座標鉛直速度
-座標鉛直速度 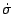 を定義する.
を定義する.
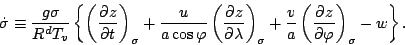 |
(105) |
式 (A.69) を重力ポテンシャル 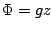 を用いて書けば,
を用いて書けば,
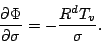 |
(106) |
水平の圧力勾配は, 式(A.71)および式(A.72) を
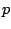 に対して適用し, 式(A.68) を用いれば次のように変換される.
に対して適用し, 式(A.68) を用いれば次のように変換される.
![\begin{displaymath}
\frac{1}{\rho} \left( \DP{p}{\varphi} \right)_z
= R^d T_v \DP[][\sigma]{\pi}{\varphi} + \DP{\Phi}{\varphi}.
\end{displaymath}](img270.png) |
(108) |
ここで
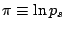 である. したがって, 運動方程室�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就厩温割儀俺激騎俺宜碍騎⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩��,
である. したがって, 運動方程室�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就厩温割儀俺激騎俺宜碍騎⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩��,
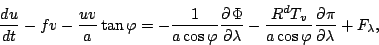 |
(109) |
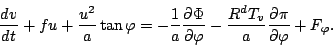 |
(110) |
速度の発散は,
ここで,
![\begin{displaymath}
\Ddiv{\Dvect{v}_H}
\equiv \frac{1}{a \cos \varphi}
\DP[]...
...hi} \left( \DP{}{\varphi} (v \cos
\varphi ) \right)_{\sigma}.
\end{displaymath}](img282.png) |
(112) |
ゆえに, 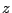 - 座標連続の式は次のように変換される.
- 座標連続の式は次のように変換される.
したがって
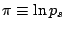 を用いて記述すれば次のようになる.
を用いて記述すれば次のようになる.
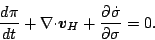 |
(114) |
式 ( A.64 ) の右辺第1項は次のように変換される.
ここで,
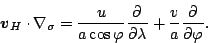 |
(116) |
したがって, 熱力学の式はつぎのようになる.
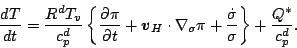 |
(117) |
ここで,  座標における境界条件について述べる.
座標における境界条件について述べる.
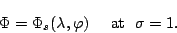 |
(118) |
すなわち,  は表面地形を表す. この境界条件を用いて, 静力学平衡
の式を鉛直積分することで, 任意の
は表面地形を表す. この境界条件を用いて, 静力学平衡
の式を鉛直積分することで, 任意の  における高度
における高度 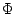 を求める
ことができる.
を求める
ことができる.
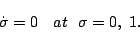 |
(119) |
ここでは述べない.
連続の式を鉛直方向に 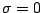 から
から 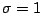 まで積分し,
まで積分し,
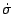 に関する境界条件を用いれば, 傾向方程式とよばれる
に関する境界条件を用いれば, 傾向方程式とよばれる 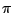 の時間変化に関する式が得られる.
の時間変化に関する式が得られる.
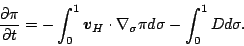 |
(120) |
この式を用いれば, 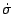 の情報がなくても地表面気圧の時間変化
を求めることができる. なお, ここでは後のことを考えて
の情報がなくても地表面気圧の時間変化
を求めることができる. なお, ここでは後のことを考えて
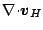 を
を 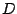 と表現している.
と表現している. 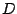 については次節で改めて
定義する.
については次節で改めて
定義する.
鉛直速度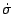 は, 連続の式を鉛直方向に
は, 連続の式を鉛直方向に 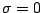 から
から
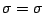 まで積分することで診断的に得られる.
まで積分することで診断的に得られる.
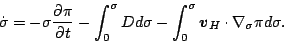 |
(121) |
11
1111
11
1111
渦度:
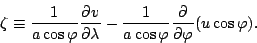 |
(122) |
発散:
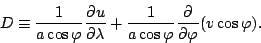 |
(123) |
運動方程式の 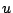 の式に
の式に
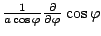 を
作用し,
を
作用し, 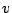 の式に
の式に
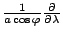 を
作用し差をとって変形すれば次の渦度方程式を得る.
を
作用し差をとって変形すれば次の渦度方程式を得る.
運動方程式の 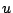 の式に
の式に
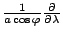 を作
用し,
を作
用し, 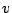 の式に
の式に
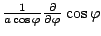 を作用し和をとって変形すると次の発散方程式を得る.
を作用し和をとって変形すると次の発散方程式を得る.
ここで,
支配方程式系における変数を, モデル内部で用いている変数に変換する. まず,
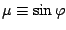 を導入する. また速度場
を導入する. また速度場 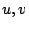 は
は
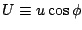 ,
,
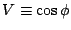 に変換する.
12 このとき, 水平風の渦度
に変換する.
12 このとき, 水平風の渦度 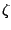 と発散
と発散 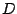 は次のように
変換され, この表現をあらためて
は次のように
変換され, この表現をあらためて 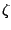 および
および 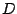 と定義する.
と定義する.
水平風による移流は次のように変換される.
水平風による移流のもうひとつの記述を連続の式の変換のために示す.
これらを用いて, 方程式系を次のように変数変換する.
連続の式
13
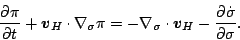 |
(132) |
渦度方程式
発散方程式
熱力学の式
水蒸気の式
仮温度 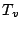 を次のように
を次のように  のみに依存する場
のみに依存する場
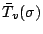 と, そこからのず釈�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就究撃崖掩訓欝⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩�
と, そこからのず釈�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就究撃崖掩訓欝⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩� 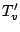 にわけて記述する.
にわけて記述する.
渦度方程式で 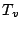 を含む項は次のように変形される。
を含む項は次のように変形される。
発散方程式で 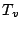 を含む項は次のように変形される.
を含む項は次のように変形される.
熱力学の式の右辺第1-3項は次のように変形される.
以上を用いて程式系を記述すれば次のようになる.
連続の式
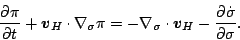 |
(140) |
静水圧の式
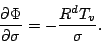 |
(141) |
運動方程式14
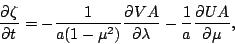 |
(142) |
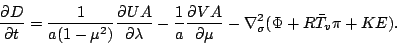 |
(143) |
ここで,
熱力学の式
水蒸気の式
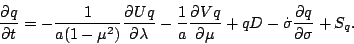 |
(147) |
式(A.17) で導入した 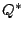 から粘性による寄与
から粘性による寄与
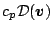 を再び分離し,
を再び分離し,
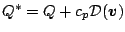 とする. 一般に粘
性は運動方程式において適当なパラメタリゼーションによって表現する. また,
渦度, 発散, 温度, 水蒸気の式に対してそれぞれ水平拡散項
とする. 一般に粘
性は運動方程式において適当なパラメタリゼーションによって表現する. また,
渦度, 発散, 温度, 水蒸気の式に対してそれぞれ水平拡散項
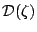 ,
,
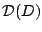 ,
,
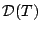 ,
,
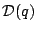 をつける.
この項の付加は主に数値的安定性の要請
によるものであるが, 物理的には後で行なう離散化のスケール以下の運動を表
現していると解釈できる. 最後に, 乾燥大気の気体定数および定圧比熱
をつける.
この項の付加は主に数値的安定性の要請
によるものであるが, 物理的には後で行なう離散化のスケール以下の運動を表
現していると解釈できる. 最後に, 乾燥大気の気体定数および定圧比熱
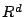 ,
, 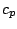 をそれぞれ
をそれぞれ 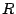 ,
, 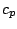 のようにあらためて置きなおせば, 支
配方程式系 (3.1) -- (3.6) を得る.
のようにあらためて置きなおせば, 支
配方程式系 (3.1) -- (3.6) を得る.
- ...
理想気体の状態方程式を用いる.4
- 乾燥空気と水蒸気は, 同じ速度と温度をもつことを暗黙のうちに仮定
している. したがって, 水蒸気に関する運動量保存則および全エネルギー保存
則および状態方程式を考慮する必要がない.
- ... 水蒸気の生成消滅を無視すれば,5
-
次で示すように水蒸気式では生成消滅を含めている. したがって, 全大気の質
量保存則は, 水蒸気の生成消滅が起きても全質量が保存するように, 乾燥大気
量が変化することを要請していることになる.
- ...
の引力によるポテンシャル6
- これは遠心力を考慮しない地球の質量にのみ起因
したポテンシャル.
- ... であるとしている.7
-
導出の過程を示す. 左辺第1項と第2項は次のように変形される.
また, 左辺第4項は次のように変形される.
- ... で近似すると8
-
この近似には疑問が残る. 状態方程式においては, 気体定数
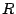 を
を 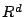 と
する近似は(仮温度
と
する近似は(仮温度 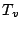 を導入することで)行なわなかった.
を導入することで)行なわなかった. 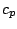 につい
てだけ近似するのは近似のレベルに一貫性がないように思われる.
につい
てだけ近似するのは近似のレベルに一貫性がないように思われる.
- ...
が成りたつ.9
-
これは自明のこととしたい. スカラー
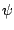 の座標変換は座標変換テンソル
に依存しない(で同じ値をとる)からである. なお, Pedlosky (1987) では, ベ
クトルの変換公式を使ってスカラーの変換を証明している. ところがベクトル
の変換公式ではスカラーの変換公式を使っているので, 何がなんだかわからな
い.
の座標変換は座標変換テンソル
に依存しない(で同じ値をとる)からである. なお, Pedlosky (1987) では, ベ
クトルの変換公式を使ってスカラーの変換を証明している. ところがベクトル
の変換公式ではスカラーの変換公式を使っているので, 何がなんだかわからな
い.
一方, ベクトルの座標変換は, 座標変換テンソルとの積で表現される. したがっ
て, 座標変換テンソル自体が時間変化する場合, 当然ベクトルの時間微分は座
標変換テンソルの時間微分の影響を受ける.
- ... これらの式は形を変えない.10
- ここで私が気になっているのは, 運動エネルギー保存の式が, 回転系へ
の移行によって形を変えることである.
- ...
動エネルギーの時間変化に寄与しないことがわかる.11
-
遠心力を重力加速度から分離してエネルギーの式で考慮すると, この寄与はキャ
ンセルすることなく残る.
- ... に変換する.12
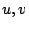 のままでも渦度や発散にすれば極での特異性を回避できる
のではないか?
のままでも渦度や発散にすれば極での特異性を回避できる
のではないか?
- ...連続の式
13
- 発散はすべて
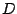 を用いて表現すべきだろう.
を用いて表現すべきだろう.
- ...
運動方程式14
- (2005/4/4 石渡)
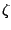 の式の右辺第一項の符号は正
しいか?
の式の右辺第一項の符号は正
しいか?  の式の右辺第二項の符号は正しいか?
の式の右辺第二項の符号は正しいか?


: 5 地球定数
: DCAPM2 第1部 数理モデル化
: 3 支配方程式・力学過程
Morikawa Yasuhiro
平成18年7月30日
![]() 33
3
33
3![]() 33
33
![]() 33
3
33
3![]() 33
33
![]() 定圧比熱を
定圧比熱を ![]() とし, 全大気の気体定数を
とし, 全大気の気体定数を ![]() とおいた. しかし, 本文
中では, 乾燥空気の気体定数を
とおいた. しかし, 本文
中では, 乾燥空気の気体定数を ![]() , 定圧比熱を
, 定圧比熱を ![]() と表記している.
と表記している.
![]() に対する質量保存則は, 単位時間単位体積あたりの生成
消滅量を
に対する質量保存則は, 単位時間単位体積あたりの生成
消滅量を ![]() とすれば,
とすれば,
![[*]](crossref.png) ) と式(A.9) から得ることができる. しかし,
今の場合, 式(A.7)で水蒸気の生成消滅を無視したので,
正しくは得られない. そこで比湿の生成消滅に関する項を改めて
) と式(A.9) から得ることができる. しかし,
今の場合, 式(A.7)で水蒸気の生成消滅を無視したので,
正しくは得られない. そこで比湿の生成消滅に関する項を改めて ![]() は圧力,
は圧力, ![]() は粘性応力テンソル,
は粘性応力テンソル, ![]() は地球
の引力によるポテンシャル
6 ,
は地球
の引力によるポテンシャル
6 , ![]() はその他の外力項である. あるいは連続の式
を用いてラグランジュ形式で記述すると
はその他の外力項である. あるいは連続の式
を用いてラグランジュ形式で記述すると
![]() と内部エ
ネルギー
と内部エ
ネルギー ![]() およぼポテンシャルエネルギー
およぼポテンシャルエネルギー ![]() の和で表
現される. この時間変化率の式は, 水蒸気の生成消滅による影響を無視すれば,
の和で表
現される. この時間変化率の式は, 水蒸気の生成消滅による影響を無視すれば,
![[*]](crossref.png) ) に
) に ![[*]](crossref.png) ) を引き去ると, 次のように内部エネルギーの式が
得られる.
) を引き去ると, 次のように内部エネルギーの式が
得られる.
![]() であ
る. さらに状態方程式 (A.5) を用いて式 (A.17)
を変形する.
であ
る. さらに状態方程式 (A.5) を用いて式 (A.17)
を変形する. ![]() であることに注意すれば
であることに注意すれば
![]() で回転する回転系に変換す
る.
で回転する回転系に変換す
る.
![]() に対して,
に対して,
![]() に対する慣性系および回転系での微分は次の関
係をもつ.
に対する慣性系および回転系での微分は次の関
係をもつ.
![]() を, 慣性系では
を, 慣性系では
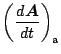
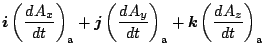
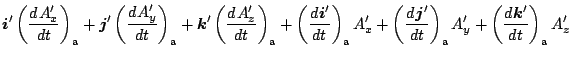

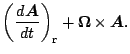
![]() (
( ![]() は位置ベクトル ) とおけば慣
性系での速度
は位置ベクトル ) とおけば慣
性系での速度
![]() (これまでの
(これまでの
![]() ) は回転系での速度
) は回転系での速度
![]() を用いて次のように表すことができる.
を用いて次のように表すことができる.
![]() において, スカラー
において, スカラー
![]() およびベクトル
およびベクトル
![]() は次のように表現
される. なお,
は次のように表現
される. なお, ![]() は各軸方向の規模因子であり, 各軸方向の基底ベクトル
は
は各軸方向の規模因子であり, 各軸方向の基底ベクトル
は ![]() とする.
とする.
![\begin{displaymath}
\DD{\Dvect{v}}{t}
= \sum^3_{k=1} \Dvect{e}_k
\left[ \DP{v...
...{v_k}{h_k} \frac{1}{h_j} \DP{h_k}{\xi_j} \right) v_j
\right].
\end{displaymath}](img179.png)
![]() が地球中心を向いているとみなして, 方程式系を球
座標
が地球中心を向いているとみなして, 方程式系を球
座標
![]() に変換する. 回転
系に固定した直交直線座標
に変換する. 回転
系に固定した直交直線座標
![]() との関係は
との関係は
![$\displaystyle \Dvect{e}_{\lambda} \frac{1}{r}
\left[ \DP{A_r}{\varphi} - \DP{}{r}(r A_{\varphi})
\right]$](img198.png)
![$\displaystyle + \Dvect{e}_{\varphi} \frac{1}{r \cos \varphi}
\left[ \DP{}{r} (r \cos \varphi A_{\lambda}) -
\DP{A_r}{\lambda} \right]$](img199.png)
![$\displaystyle + \Dvect{e}_r \frac{1}{r \cos \varphi}
\left[ \DP{A_{\varphi}}{\lambda} - \DP{}{\varphi} (\cos
\varphi A_{\lambda}) \right],$](img200.png)
![$\displaystyle \Dvect{e}_{\lambda} \left[
\DP{A_{\lambda}}{t} + \frac{u}{r \cos ...
..._{\lambda}}{r}
+ \frac{u}{r} A_r - \frac{u \tan \varphi}{r} A_{\varphi} \right]$](img203.png)
![$\displaystyle + \Dvect{e}_{\varphi} \left[
\DP{A_{\varphi}}{t} + \frac{u}{r \co...
..._{\varphi}}{r}
+ \frac{v}{r} A_r + \frac{u \tan \varphi}{r} A_{\lambda} \right]$](img204.png)
![$\displaystyle + \Dvect{e}_r \left[
\DP{A_r}{t} + \frac{u}{r \cos \varphi} \DP{A...
...i} + w \DP{A_r}{r}
- \frac{v}{r} A_{\varphi} - \frac{u}{r} A_{\lambda} \right].$](img205.png)
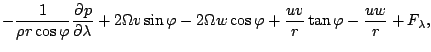
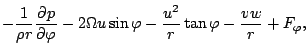
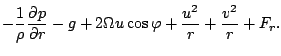
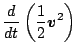
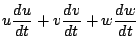
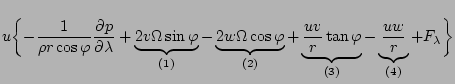
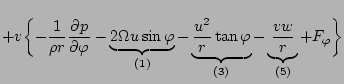

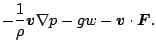
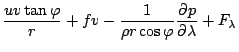
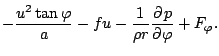
![]() を, 代表的
な地球半径
を, 代表的
な地球半径 ![]() でおきかえる. また,
でおきかえる. また, ![]() による微分はすべて海抜高度
による微分はすべて海抜高度 ![]() による微分でおきかえる. このとき基礎方程式は次のようになる.
による微分でおきかえる. このとき基礎方程式は次のようになる.
![]() は鉛直座標
は鉛直座標 ![]() に対し単調減少する関数で
ある. そこで, 鉛直座標を
に対し単調減少する関数で
ある. そこで, 鉛直座標を ![]() から, 地表面気圧
から, 地表面気圧 ![]() で規格化した気圧座
標,
で規格化した気圧座
標,
![]() - 座標から
- 座標から ![]() - 座標への変換公式を示す.
- 座標への変換公式を示す.
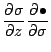
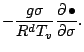
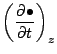
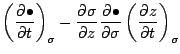

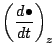
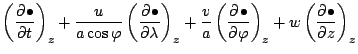
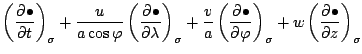
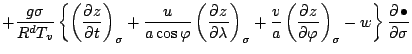
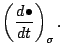
![]() を用いて書けば,
を用いて書けば,
![]() に対して適用し, 式(A.68) を用いれば次のように変換される.
に対して適用し, 式(A.68) を用いれば次のように変換される.
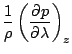
![$\displaystyle \frac{1}{\rho} \left\{ \DP[][\sigma]{p}{\lambda}
+ \frac{g \sigma}{R^d T_v} \DP{p}{\sigma} \DP[][\sigma]{z}{\lambda}
\right\}$](img267.png)
![$\displaystyle \frac{R^d T_v}{p_s} \DP{p_s}{\lambda}
+ \frac{R^d T_v}{p} \frac{g \sigma}{R^d T_v} p_s \DP[][\sigma]{z}{\lambda}$](img268.png)
![$\displaystyle R^d T_v \DP[][\sigma]{\pi}{\lambda} + \DP{\Phi}{\lambda},$](img269.png)
![$\displaystyle \frac{1}{a \cos \varphi}
\left[ \DP[][\sigma]{u}{\lambda}
+ \frac{g \sigma}{R^d T_v} \DP{u}{\sigma}
\DP[][\sigma]{z}{\lambda} \right]$](img275.png)
![$\displaystyle + \frac{1}{a \cos \varphi}
\left[ \left( \DP{}{\varphi} (v \cos \...
...ght]
- \frac{g \sigma}{R^d T_v} \DP{}{\sigma} \left( \DD{z}{t}
\right)_{\sigma}$](img276.png)
![$\displaystyle \frac{1}{a \cos \varphi}
\left[ \DP[][\sigma]{u}{\lambda}
+ \frac{g \sigma}{R^d T_v} \DP{u}{\sigma}
\DP[][\sigma]{z}{\lambda} \right]$](img275.png)
![$\displaystyle + \frac{1}{a \cos \varphi}
\left[ \left( \DP{}{\varphi} (v \cos \...
...igma}{R^d T_v}\DP{}{\sigma} ( v \cos \varphi)
\DP[][\sigma]{z}{\lambda} \right]$](img277.png)
![$\displaystyle - \frac{g \sigma}{R^d T_v} \DP{}{\sigma} \left[
\DP[][\sigma]{z}{...
...}
+ \frac{v}{a} \DP[][\sigma]{z}{\varphi}
+ \dot{\sigma} \DP{z}{\sigma}
\right]$](img278.png)
![$\displaystyle \frac{1}{a \cos \varphi} \DP[][\sigma]{u}{\lambda}
+ \frac{1}{a \...
...t( \DP{}{\varphi} (v \cos
\varphi) \right)_{\sigma}
+ \DP{\dot{\sigma}}{\sigma}$](img279.png)
![$\displaystyle - \frac{g \sigma}{R^d T_v} \left[ \DP{}{\sigma} \DP[][\sigma]{z}{...
...P[][\sigma]{z}{\varphi}
+ \dot{\sigma} \DP{}{\sigma} \DP[][]{z}{\sigma} \right]$](img280.png)
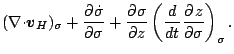
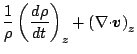
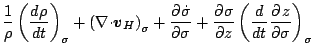
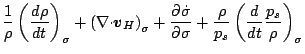
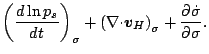
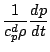
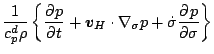
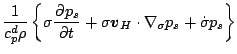

![]() 座標における境界条件について述べる.
座標における境界条件について述べる.
![]() から
から ![]() まで積分し,
まで積分し,
![]() に関する境界条件を用いれば, 傾向方程式とよばれる
に関する境界条件を用いれば, 傾向方程式とよばれる ![]() の時間変化に関する式が得られる.
の時間変化に関する式が得られる.
![]() は, 連続の式を鉛直方向に
は, 連続の式を鉛直方向に ![]() から
から
![]() まで積分することで診断的に得られる.
まで積分することで診断的に得られる.
![]() の式に
の式に
![]() を
作用し,
を
作用し, ![]() の式に
の式に
![]() を
作用し差をとって変形すれば次の渦度方程式を得る.
を
作用し差をとって変形すれば次の渦度方程式を得る.
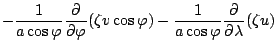
![$\displaystyle - \frac{1}{a \cos \varphi} \DP{}{\lambda}
\left[ \dot{\sigma} \DP{v}{\sigma}
+ \frac{R^d T_v}{a p_s} \DP{p_s}{\varphi}
- F_{\varphi} + f u \right]$](img315.png)
![$\displaystyle - \frac{1}{a \cos \varphi} \DP{}{\varphi}
\left[ - \cos \varphi \...
...a p_s} \DP{p_s}{\lambda}
+ F_{\lambda} \cos \varphi + f v \cos \varphi \right].$](img316.png)
![]() の式に
の式に
![]() を作
用し,
を作
用し, ![]() の式に
の式に
![]() を作用し和をとって変形すると次の発散方程式を得る.
を作用し和をとって変形すると次の発散方程式を得る.
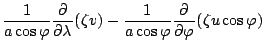
![$\displaystyle - \frac{1}{a \cos \varphi} \DP{}{\lambda}
\left[ \dot{\sigma} \DP...
...frac{R^d T_v}{a \cos \varphi p_s} \DP{p_s}{\lambda}
- F_{\lambda} - f v \right]$](img319.png)
![$\displaystyle - \frac{1}{a \cos \varphi} \DP{}{\varphi}
\left[ \cos \varphi \do...
..._s}{\varphi} \cos \varphi
- F_{\varphi} \cos \varphi + f u \cos \varphi \right]$](img320.png)
![$\displaystyle \frac{1}{a^2 \cos^2 \varphi} \DP[2]{}{\lambda}
+ \frac{1}{a^2 \cos \varphi} \DP{}{\varphi} ( \cos
\varphi \DP{}{\varphi} ),$](img323.png)
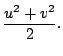
![]() を導入する. また速度場
を導入する. また速度場 ![]() は
は
![]() ,
,
![]() に変換する.
12 このとき, 水平風の渦度
に変換する.
12 このとき, 水平風の渦度 ![]() と発散
と発散 ![]() は次のように
変換され, この表現をあらためて
は次のように
変換され, この表現をあらためて ![]() および
および ![]() と定義する.
と定義する.
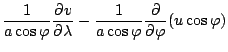
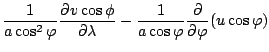
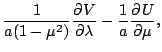
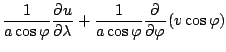
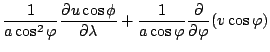
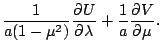
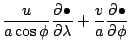
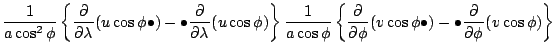

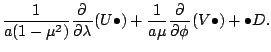
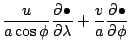
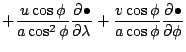
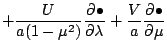
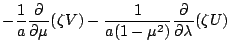
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ \dot{\sigma} \DP{V}...
...ac{R^d T_v}{a} (1-\mu^2) \DP{\pi}{\mu}
- F_{\varphi} \cos \varphi + f U \right]$](img346.png)
![$\displaystyle - \frac{1}{a} \DP{}{\mu}
\left[ - \dot{\sigma} \DP{U}{\sigma}
- \frac{R^d T_v}{a} \DP{\pi}{\lambda}
+ F_{\lambda} \cos \varphi + fV \right].$](img347.png)
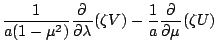
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ \dot{\sigma} \DP{U}...
...
+ \frac{R^d T_v}{a} \DP{\pi}{\lambda}
- F_{\lambda} \cos \varphi - f V \right]$](img349.png)
![$\displaystyle - \frac{1}{a} \DP{}{\mu}
\left[ \dot{\sigma} \DP{V}{\sigma}
+ \frac{R^d T_v}{a} ( 1-\mu^2 ) \DP{\pi}{\mu}
- F_{\varphi} \cos \varphi + f U \right]$](img350.png)
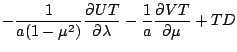
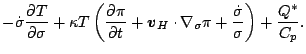
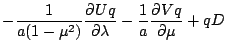
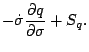
![]() を次のように
を次のように ![]() のみに依存する場
のみに依存する場
![]() と, そこからのず釈�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就究撃崖掩訓欝⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩�
と, そこからのず釈�蓿繙就�粮㏍芍��轣蛹≒鳫�笏蜿遐�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就究撃崖掩訓欝⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿畩� ![]() にわけて記述する.
にわけて記述する.
![]() を含む項は次のように変形される。
を含む項は次のように変形される。
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ + \frac{R^d T_v}{a}...
...]
- \frac{1}{a} \DP{}{\mu}
\left[ - \frac{R^d T_v}{a} \DP{\pi}{\lambda} \right]$](img359.png)
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ + \frac{R^d \bar{T}...
...^2)} \DP{}{\lambda}
\left[ + \frac{R^d T'_v}{a} (1-\mu^2) \DP{\pi}{\mu} \right]$](img360.png)
![$\displaystyle - \frac{1}{a} \DP{}{\mu}
\left[ - \frac{R^d \bar{T}_v}{a} \DP{\pi...
...
- \frac{1}{a} \DP{}{\mu}
\left[ - \frac{R^d T'_v}{a} \DP{\pi}{\lambda} \right]$](img361.png)
![$\displaystyle - \frac{1}{a} \frac{R^d \bar{T}_v}{a}
\frac{\partial^2 \pi}{\part...
...^2)} \DP{}{\lambda}
\left[ + \frac{R^d T'_v}{a} (1-\mu^2) \DP{\pi}{\mu} \right]$](img362.png)
![$\displaystyle + \frac{1}{a} \frac{R^d \bar{T}_v}{a}
\frac{\partial^2 \pi}{\part...
...
- \frac{1}{a} \DP{}{\mu}
\left[ - \frac{R^d T'_v}{a} \DP{\pi}{\lambda} \right]$](img363.png)
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ + \frac{R^d T'_v}{a...
...- \frac{1}{a} \DP{}{\mu}
\left[ - \frac{R^d T'_v}{a} \DP{\pi}{\lambda} \right].$](img364.png)
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ \frac{R^d T_v}{a} \...
...rac{1}{a} \DP{}{\mu}
\left[ \frac{R^d T_v}{a} ( 1-\mu^2 ) \DP{\pi}{\mu} \right]$](img365.png)
![$\displaystyle - \frac{1}{a (1-\mu^2)} \DP{}{\lambda}
\left[ \frac{R^d \bar{T}_v...
...a (1-\mu^2)} \DP{}{\lambda}
\left[ \frac{R^d T'_v}{a} \DP{\pi}{\lambda} \right]$](img366.png)
![$\displaystyle - \frac{1}{a} \DP{}{\mu}
\left[ \frac{R^d \bar{T}_v}{a} ( 1-\mu^2...
...ac{1}{a} \DP{}{\mu}
\left[ \frac{R^d T'_v}{a} ( 1-\mu^2 ) \DP{\pi}{\mu} \right]$](img367.png)
![$\displaystyle - \frac{1}{a^2 (1-\mu^2)} \DP[2]{}{\lambda}
( R^d \bar{T}_v \pi )...
...a (1-\mu^2)} \DP{}{\lambda}
\left[ \frac{R^d T'_v}{a} \DP{\pi}{\lambda} \right]$](img368.png)
![$\displaystyle - \frac{1}{a^2} \DP{}{\mu}
\left[ (1-\mu^2) \DP{}{\mu} ( R^d \bar...
...ac{1}{a} \DP{}{\mu}
\left[ \frac{R^d T'_v}{a} ( 1-\mu^2 ) \DP{\pi}{\mu} \right]$](img369.png)
![$\displaystyle - \Dgrad^2_{\sigma} ( R^d \bar{T}_v \pi )
- \frac{1}{a (1-\mu^2)}...
...c{1}{a} \DP{}{\mu}
\left[ \frac{R^d T'_v}{a} ( 1-\mu^2 ) \DP{\pi}{\mu} \right].$](img370.png)
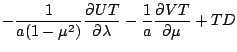
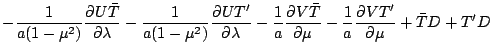
![$\displaystyle - \frac{\bar{T}}{a(1-\mu^{2})} \DP{U}{\lambda}
- \frac{1}{a(1-\mu...
...1}{a(1-\mu^{2})} \DP{U}{\lambda}
+ \frac{\bar{1}}{a} \DP{V}{\mu} \right]
+ T' D$](img372.png)
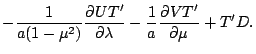
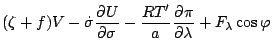
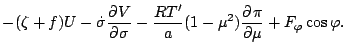
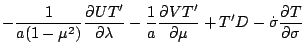
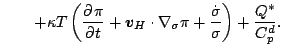
![]() から粘性による寄与
から粘性による寄与
![]() を再び分離し,
を再び分離し,
![]() とする. 一般に粘
性は運動方程式において適当なパラメタリゼーションによって表現する. また,
渦度, 発散, 温度, 水蒸気の式に対してそれぞれ水平拡散項
とする. 一般に粘
性は運動方程式において適当なパラメタリゼーションによって表現する. また,
渦度, 発散, 温度, 水蒸気の式に対してそれぞれ水平拡散項
![]() ,
,
![]() ,
,
![]() ,
,
![]() をつける.
この項の付加は主に数値的安定性の要請
によるものであるが, 物理的には後で行なう離散化のスケール以下の運動を表
現していると解釈できる. 最後に, 乾燥大気の気体定数および定圧比熱
をつける.
この項の付加は主に数値的安定性の要請
によるものであるが, 物理的には後で行なう離散化のスケール以下の運動を表
現していると解釈できる. 最後に, 乾燥大気の気体定数および定圧比熱
![]() ,
, ![]() をそれぞれ
をそれぞれ ![]() ,
, ![]() のようにあらためて置きなおせば, 支
配方程式系 (3.1) -- (3.6) を得る.
のようにあらためて置きなおせば, 支
配方程式系 (3.1) -- (3.6) を得る.