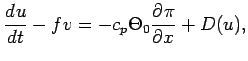 |
(1) | ||
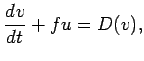 |
(2) | ||
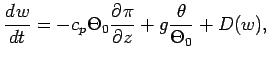 |
(3) | ||
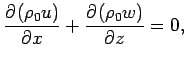 |
(4) | ||
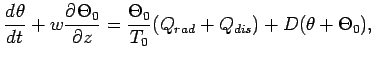 |
(5) | ||
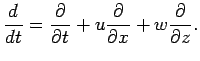 |
大気は回転系の 2 次元の非弾性方程式系(Ogura and Phllips, 1962)でモデル化 する.
(1), (2), (3)は運動方
程式, (4)は連続の式, (5)は熱力学の式である.
![]() は水平座標,
は水平座標, ![]() は鉛直および時間座標,
は鉛直および時間座標, ![]() は水平風速,
は水平風速, ![]() は
鉛直風速,
は
鉛直風速, ![]() はそれぞれ温位と無次元圧力関数の基本場からの偏
差である. このモデルでは
はそれぞれ温位と無次元圧力関数の基本場からの偏
差である. このモデルでは ![]() 方向に一様な 2 次元場を想定している.
方向に一様な 2 次元場を想定している.
![]() はそれぞれ基本場の密度と温位, 温度である.
はそれぞれ基本場の密度と温位, 温度である. ![]() はコリオリパラメータ,
はコリオリパラメータ, ![]() は重力加速度である.
は重力加速度である. ![]() は放射加熱(冷却)
であり, 後述の放射過程により与えられる.
は放射加熱(冷却)
であり, 後述の放射過程により与えられる. ![]() は散逸加熱であり, 後
述の乱流モデルから与えられる.
は散逸加熱であり, 後
述の乱流モデルから与えられる.
(1)![]() (5)式中の
(5)式中の ![]() 項は数
値モデルの空間格子間隔以下の乱流による混合の寄与で, 以下のように表される.
項は数
値モデルの空間格子間隔以下の乱流による混合の寄与で, 以下のように表される.
ここで ![]() は(10), (11)式で計
算される乱流拡散係数である.
は(10), (11)式で計
算される乱流拡散係数である.
無次元圧力関数 ![]() と温位
と温位 ![]() は以下の式で定義される.
は以下の式で定義される.
![[*]](crossref.png) )式を変形して得られる以下の式から診断される.
)式を変形して得られる以下の式から診断される.
境界条件は ![]() 方向に周期境界条件, 大気下端では
方向に周期境界条件, 大気下端では ![]() , 大気上端では応力
なし条件を与える. 大気下端の運動量フラックスと熱フラックスの境界条件は乱
流モデルによって計算される.
, 大気上端では応力
なし条件を与える. 大気下端の運動量フラックスと熱フラックスの境界条件は乱
流モデルによって計算される.
大気モデル部分に現れるパラメータの標準設定は以下のようになっている.
| パラメータ | 標準値 | 備考 |
| 0 sec |
||
| 3.72 msec |
火星の平均値 | |
| 7 hPa | 火星の平均地表気圧 | |
| 734.9 Jkg |
CO |
|
| 189.0 Jkg |
CO |