この節では空間微分の離散化の方法とそのために必要となる平均操作, 境界条 件の与え方について説明する. 離散化は 2 次精度差分または 4 次精度差分を 用いて行う.
Fig.1.1 の空間の位置を表す添字として,
![]() 方向フラックスの格子点を (
方向フラックスの格子点を (![]() ),
),
![]() 方向フラックスの格子点を (
方向フラックスの格子点を (![]() ),
スカラー量の格子点を (
),
スカラー量の格子点を (![]() ),
格子の角に当たる点を (
),
格子の角に当たる点を (![]() ) とする
(Fig.1.1 参照).
但し
) とする
(Fig.1.1 参照).
但し
![]() ,
,
![]() ,
,
![]() ,
,
![]() である.
である.
空間微分の離散化を行う前に, そのために必要となる平均操作を定義しておく.
例えば ![]() 方向フラックス格子点で評価される変数をスカラー量の格子点で評
価する場合は, フラックス格子点の値を平均してスカラー格子点での値とみなす.
方向フラックス格子点で評価される変数をスカラー量の格子点で評
価する場合は, フラックス格子点の値を平均してスカラー格子点での値とみなす.
必要となる平均操作を以下に示す. ここでは ![]() 方向のフラックス格子点の変
数を
方向のフラックス格子点の変
数を ![]() ,
, ![]() 方向のフラックス格子点の変数を
方向のフラックス格子点の変数を ![]() , ス
カラー格子点の変数を
, ス
カラー格子点の変数を ![]() としている.
としている.
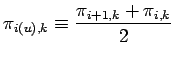 |
(2.1) | ||
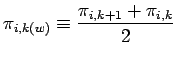 |
(2.2) | ||
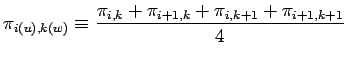 |
(2.3) | ||
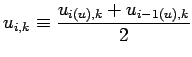 |
(2.4) | ||
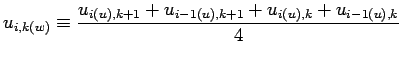 |
(2.5) | ||
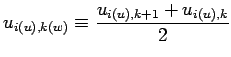 |
(2.6) | ||
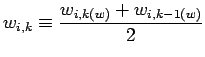 |
(2.7) | ||
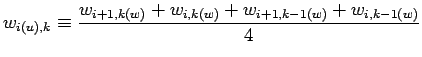 |
(2.8) | ||
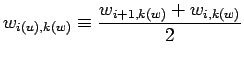 |
(2.9) |
空間微分を 2 次精度差分で離散化する際に必要となる微分操作を以下に示す.
ここでは ![]() 方向のフラックス格子点の変数を
方向のフラックス格子点の変数を ![]() ,
,
![]() 方向のフラックス格子点の変数を
方向のフラックス格子点の変数を ![]() ,
スカラー格子点の変数を
,
スカラー格子点の変数を ![]() としている.
としている.
![]() ,
, ![]() 方向ともにフラックス格子点の変数を
方向ともにフラックス格子点の変数を
![]() としている.
としている.
それぞれの変数に対して微分を評価する格子点は一意に決まる.
そのため, 他の格子点において微分を評価する場合には平均操作を用いる.
![$\displaystyle \left[\DP{\pi}{x} \right]_{i(u),k}
\equiv \frac{\pi_{i+1, k} - \pi_{i, k}}{\Delta x}$](img32.png) |
(2.10) | ||
![$\displaystyle \left[\DP{\pi}{z} \right]_{i,k(w)}
\equiv \frac{\pi_{i, k+1} - \pi_{i, k}}{\Delta z}$](img33.png) |
(2.11) | ||
![$\displaystyle \left[\DP{u}{x} \right]_{i,k}
\equiv \frac{u_{i(u), k} - u_{i-1(u), k}}{\Delta x}$](img34.png) |
(2.12) | ||
![$\displaystyle \left[\DP{u}{z} \right]_{i(u),k(w)}
\equiv \frac{u_{i(u), k+1} - u_{i(u), k}}{\Delta z}$](img35.png) |
(2.13) | ||
![$\displaystyle \left[\DP{w}{x} \right]_{i(u),k(w)}
\equiv \frac{w_{i+1, k(w)} - w_{i, k(w)}}{\Delta x}$](img36.png) |
(2.14) | ||
![$\displaystyle \left[\DP{w}{z} \right]_{i,k}
\equiv \frac{w_{i, k(w)} - w_{i, k-1(w)}}{\Delta z}$](img37.png) |
(2.15) | ||
![$\displaystyle \left[\DP{\phi}{x} \right]_{i,k(w)}
\equiv \frac{\phi_{i(u), k(w)} - \phi_{i-1(u), k(w)}}{\Delta x}$](img38.png) |
(2.16) | ||
![$\displaystyle \left[\DP{\phi}{z} \right]_{i(u),k}
\equiv \frac{\phi_{i(u), k(w)} - \phi_{i(u), k-1(w)}}{\Delta z}$](img39.png) |
(2.17) |
2 次精度中心差分の場合と同様に, 空間微分を 4 次精度差分で離散化する際 に必要となる微分操作を以下に示す.
![$\displaystyle \left[\DP{\pi}{x} \right]_{i(u),k}
\equiv \frac{9}{8}\left(\frac{...
...\right) -
\frac{1}{24}\left(\frac{\pi_{i+2, k} - \pi_{i-1, k}}{\Delta x}\right)$](img40.png) |
(2.18) | ||
![$\displaystyle \left[\DP{\pi}{z} \right]_{i,k(w)}
\equiv \frac{9}{8}\left(\frac{...
...\right) -
\frac{1}{24}\left(\frac{\pi_{i, k+2} - \pi_{i, k-1}}{\Delta x}\right)$](img41.png) |
(2.19) | ||
![$\displaystyle \left[\DP{u}{x} \right]_{i,k}
\equiv \frac{9}{8}\left(\frac{u_{i(...
...ight) -
\frac{1}{24}\left(\frac{u_{i(u)+1, k} - u_{i-2(u), k}}{\Delta x}\right)$](img42.png) |
(2.20) | ||
![$\displaystyle \left[\DP{u}{z} \right]_{i(u),k(w)}
\equiv \frac{9}{8}\left(\frac...
...ight) -
\frac{1}{24}\left(\frac{u_{i(u), k+2} - u_{i(u), k-1}}{\Delta x}\right)$](img43.png) |
(2.21) | ||
![$\displaystyle \left[\DP{w}{x} \right]_{i(u),k(w)}
\equiv \frac{9}{8}\left(\frac...
...ight) -
\frac{1}{24}\left(\frac{w_{i+2, k(w)} - w_{i-1, k(w)}}{\Delta x}\right)$](img44.png) |
(2.22) | ||
![$\displaystyle \left[\DP{w}{z} \right]_{i,k}
\equiv \frac{9}{8}\left(\frac{w_{i,...
...ight) -
\frac{1}{24}\left(\frac{w_{i, k+1(w)} - w_{i, k-2(w)}}{\Delta z}\right)$](img45.png) |
(2.23) | ||
![$\displaystyle \left[\DP{\phi}{x} \right]_{i,k(w)}
\equiv \frac{9}{8}
\left(\fra...
...{1}{24}
\left(\frac{\phi_{i+1(u), k(w)} - \phi_{i-2(u), k(w)}}{\Delta x}\right)$](img46.png) |
(2.24) | ||
![$\displaystyle \left[\DP{\phi}{z} \right]_{i(u),k}
\equiv \frac{9}{8}\left(
\fra...
...{1}{24}\left(
\frac{\phi_{i(u), k+1(w)} - \phi_{i(u), k-2(w)}}{\Delta z}\right)$](img47.png) |
(2.25) |
![\begin{displaymath}
\left[\DP{\overline{\pi}}{z}\right]_{i,k} =
- \frac{g}{{c_{p}}_{d} [\overline{\theta_{v}}]_{i,k}}
\end{displaymath}](img48.png) |
(2.26) |
![\begin{displaymath}
\overline{\rho}_{i,k} = \frac{p_{0}}{R_{d}}
\frac{[\overline{\pi}^{c_{v}/R_{d}}]_{i,k}}
{[\overline{\theta_{v}}]_{i,k}}
\end{displaymath}](img50.png) |
(2.27) |
| (2.31) |
ここでは離散化した変数に対する境界条件の与え方をまとめる. 考慮する境界条 件は, 周期境界条件, 境界ですべりなし条件と応力なし条件である.
例として, ![]() 方向フラックス格子点に配置された変数
方向フラックス格子点に配置された変数 ![]() を考える.
計算領域内の
を考える.
計算領域内の ![]() 方向の添字を
方向の添字を
![]() とし, 糊代部分の格子点数
を
とし, 糊代部分の格子点数
を ![]() とする(Fig.1.2参照). このとき周期境界条件は以下のように与
えられる.
とする(Fig.1.2参照). このとき周期境界条件は以下のように与
えられる.
| (2.36) | |||
| (2.37) | |||
| (2.38) | |||
| (2.39) |
![]() 方向フラックス格子点に配置された変数, スカラー格子点に配置された変数
に対しても同様に与えることができる.
方向フラックス格子点に配置された変数, スカラー格子点に配置された変数
に対しても同様に与えることができる.
境界で速度を 0 とする. この場合, 境界をはさんで変数の値が反対称になるよ うに与える.
例として ![]() 方向に境界を与えた場合を考える.
方向に境界を与えた場合を考える. ![]() 方向フラックス格子点に
配置された変数に対しては.
方向フラックス格子点に
配置された変数に対しては.
| (2.40) | |||
| (2.41) | |||
| (2.42) | |||
| (2.43) |
| (2.44) | |||
| (2.45) | |||
| (2.46) | |||
| (2.47) |
境界上で法線方向速度を 0, 接線方向速度の法線方向微分を 0 とする. この場 合, 境界上で配首鞜�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就羆皺畄箋禊箋剛箋竇盂粭盍畍皹粭矜⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵は境界をはさんで変数の値が反対称になるよう に与え, 境界上に配置されていない変数に対しては壁をはさんで変数の値が対称 になるように与える.
例として ![]() 方向に境界を与えた場合を考える.
方向に境界を与えた場合を考える. ![]() 方向フラックス格子点に
配置された変数に対しては.
方向フラックス格子点に
配置された変数に対しては.
| (2.48) | |||
| (2.49) | |||
| (2.50) | |||
| (2.51) |
| (2.52) | |||
| (2.53) | |||
| (2.54) | |||
| (2.55) |