
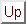

: B. 乱流パラメタリゼーション
: 湿潤大気における 2 次元非静力学モデルの定式化
: 2. 参考文献
地球大気における湿潤対流の定式化同様, 大気の乾首鞜�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就昂箒羂箏盥粐⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵と湿首鞜�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就梓街教幹過翫⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の
分子量の差は密度の式には考慮するが, 熱の式には考慮しないような
系を考える. この系では大気の熱エネルギーは乾燥大気の熱エネルギーで
決まることになる. このような系では温位 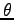 が保存量として使える.
が保存量として使える.
水平鉛直 2 次元大気の状態を
気温 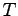 , 圧力
, 圧力 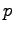 , 風速
, 風速 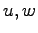 , 密度
, 密度  で表現する場合,
基礎方程式系は以下のようになる.
で表現する場合,
基礎方程式系は以下のようになる.
- 運動方程式
-
| |
|
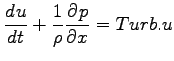 |
(A.1) |
| |
|
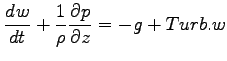 |
(A.2) |
- 連続の式
-
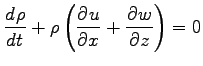 |
|
|
(A.3) |
- 密度の式(状態方程式)
-
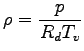 |
|
|
(A.4) |
- 熱の式
-
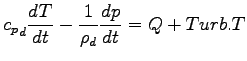 |
|
|
(A.5) |
- �$B6E=L@.J,$N:.9gHfJ]B8<0
-
ここで 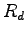 ,
, 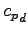 ,
, 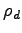 は単位質量当たりの乾燥成分の
気体定数, 定圧比熱, 密度であり,
は単位質量当たりの乾燥成分の
気体定数, 定圧比熱, 密度であり,
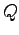 は非断熱加熱,
は非断熱加熱, 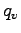 �$B$O5$BN@.J,$N:.9gHf,
�$B$O5$BN@.J,$N:.9gHf,
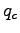 は雲水混合比,
は雲水混合比,
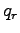 は雨水混合比である.
は雨水混合比である.
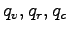 は, �$B6E=L@.J,$N?t$@$1B8:_$9$k.
は, �$B6E=L@.J,$N?t$@$1B8:_$9$k.
 ,
, 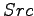 ,
, 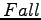 を付けた項はそれぞれ
拡散項, 生成消滅項, 落下項を意味する.
を付けた項はそれぞれ
拡散項, 生成消滅項, 落下項を意味する.
密度の室齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就教亀官峨官過騎屋妓温乙癌我⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の混合比が考慮されている.
ただし,
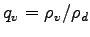 ,
, 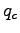 ,
, 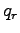 はそれぞれ,
凝縮性気体, 雲水, 雨水の混合比を意味する. ここで乾首鞜�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就教牡芦乙癌我⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の分圧
はそれぞれ,
凝縮性気体, 雲水, 雨水の混合比を意味する. ここで乾首鞜�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就教牡芦乙癌我⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の分圧 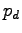 は.
は.
となるので,
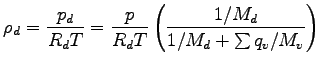 |
|
|
(A.10) |
である. 但し 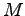 は分子量を表し, �$B6E=L@.J,$NBN@Q$OL5;k$G$-$k$b$N$H8+$J$7$?.
(A.9), (A.10) 式より,
は分子量を表し, �$B6E=L@.J,$NBN@Q$OL5;k$G$-$k$b$N$H8+$J$7$?.
(A.9), (A.10) 式より,
となる.
と定義すると, (A.11) 式は以下のように書ける.
また, 温位とエクスナー関数を用いて表現すると,
である. 但しエクスナー関数 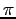 は
は
 の関係を満たす.
の関係を満たす.
温位は乾燥断熱状態における保存量である.
乾燥断熱状態を表す熱力学の式は
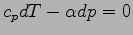 |
|
|
(A.14) |
である. ここで 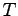 は温度,
は温度, 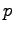 は圧力,
は圧力,
 は単位質量当たりの比熱,
は単位質量当たりの比熱, 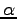 は比容である.
(A.14) 式の
は比容である.
(A.14) 式の 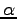 は,
理想気体の状態方程式を用いると,
は,
理想気体の状態方程式を用いると,
 |
|
|
(A.15) |
と書ける. ここで 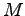 は分子量,
は分子量, 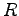 は気体定数である.
(A.14) 式に (A.15) 式を代入し整理すると,
は気体定数である.
(A.14) 式に (A.15) 式を代入し整理すると,
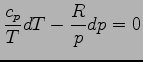 |
|
|
(A.16) |
となる. 凝縮を生じない場合には気塊の組成は変化しないので
 と
と 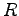 は共に
は共に 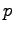 に依存しない.
一般に
に依存しない.
一般に  は
は 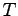 の関数であるが,
の関数であるが,
 を定数とみなすと,
を定数とみなすと,
となり, 温位が得られる.
水平鉛直 2 次元大気の状態を
温位 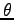 , 圧力
, 圧力 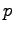 , 風速
, 風速 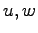 , 密度
, 密度  で表現する場合,
基礎方程式系は以下のようになる.
CReSS(坪木と榊原, 2001)では,
この基礎方程式を用いている.
で表現する場合,
基礎方程式系は以下のようになる.
CReSS(坪木と榊原, 2001)では,
この基礎方程式を用いている.
- 運動方程式
-
| |
|
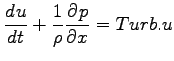 |
(A.18) |
| |
|
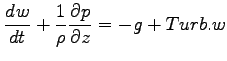 |
(A.19) |
- 圧力方程式
-
 |
|
|
(A.20) |
- 密度の式(状態方程式)
-
 |
|
|
(A.21) |
- 熱の式
-
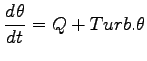 |
|
|
(A.22) |
- �$B6E=L@.J,$N:.9gHf$NJ]B8<0
-
ただし温位 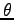 は
は
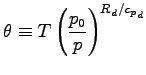 |
|
|
(A.26) |
であり, 仮温位  は,
は,
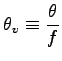 |
|
|
(A.27) |
である. 音速 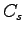 は
は
 |
|
|
(A.28) |
である. 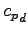 と
と  はそれぞれ単位質量当たりの
乾燥成分の定圧比熱と定積比熱であり,
はそれぞれ単位質量当たりの
乾燥成分の定圧比熱と定積比熱であり,
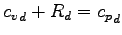 という
関係にある.
という
関係にある.
圧力方程式は密度の式と連続の式を組み合わせることで得られる.
まず密度を
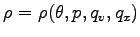 として
として
 の全微分を求める.
の全微分を求める.
となる. (A.29) 式を圧力の式として整理すると,
であり, 連続の式を用いると,
となり, 圧力方程式が得られる.
水平鉛直 2 次元大気の状態を
温位 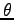 , 無次元圧力
, 無次元圧力 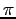 , 風速
, 風速 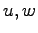 , 密度
, 密度  で表現する場合,
基礎方程式系は以下のようになる.
連続の式 (A.3) と状態方程式 (A.21)
を用いることで得られる圧力方程式を利用する.
Klemp and Willhelmson (1978)では, この基礎方程式を用いている.
で表現する場合,
基礎方程式系は以下のようになる.
連続の式 (A.3) と状態方程式 (A.21)
を用いることで得られる圧力方程式を利用する.
Klemp and Willhelmson (1978)では, この基礎方程式を用いている.
- 運動方程式
-
| |
|
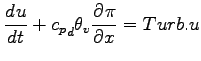 |
(A.30) |
| |
|
 |
(A.31) |
- 圧力方程式
-
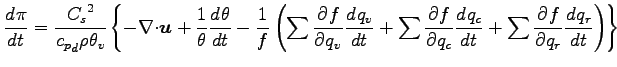 |
|
|
(A.32) |
- 状態方程式
-
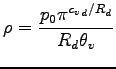 |
|
|
(A.33) |
- 熱の式
-
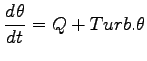 |
|
|
(A.34) |
- 水蒸気および水物質混合比の式
-
ただし, エクスナー関数 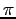 は,
は,
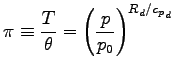 |
|
|
(A.38) |
であり, 音速 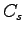 は
は
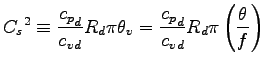 |
|
|
(A.39) |
である.
運動方程式の圧力勾配は, 温位とエクスナー関数を用いることで得られる.
圧力方程式は密度の式と連続の式を組み合わせることで得られる.
まず密度を
 として
として
 の全微分を計算する.
の全微分を計算する.
となる. (A.41) 式を圧力の式として整理すると,
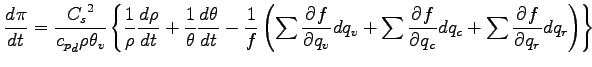 |
|
|
(A.42) |
となり, 連続の式を用いると,
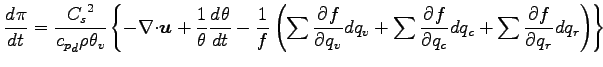 |
|
|
(A.43) |
となり, 圧力方程式が得られる.
準圧縮方程式系では, 変数を基本場と擾乱場に分離し, 線形化を行う.
変数を基本場と擾乱場に分離し, 基本場は静水圧平衡にあると仮定する.
この時, 変数は以下のように書ける.
但し,
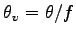 とし,
基本場の風速
とし,
基本場の風速 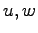 と雲粒混合比と雨粒混合はゼロと見なした.
そして基本場には静水圧平衡,
と雲粒混合比と雨粒混合はゼロと見なした.
そして基本場には静水圧平衡,
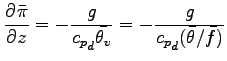 |
|
|
(A.44) |
の関係が成り立つものとする.
水平方向の運動方程式を基本場と擾乱場に分離する.
上式において移流項以外の 2 次の微小項を消去し, さらに基本場は 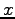 方向に
は変化しないことを利用すると, 以下の昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就籵瘁攻痰高羌恒⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の式が得られる.
方向に
は変化しないことを利用すると, 以下の昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就籵瘁攻痰高羌恒⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の式が得られる.
ここで 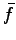 は,
は,
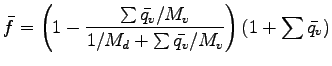 |
|
|
(A.46) |
である.
鉛直方向の運動方程式を基本場と擾乱場に分離する.
上式において移流項以外の 2 次の微小項を消去すると以下となる.
さらに静水圧の式を利用すると以下となる.
ここで
 は,
は,
であり, (A.47) 式の第 2 項を計算すると,
であり, (A.47) 式の第 3 項を計算すると,
であり, (A.47) 式の第 4 項を計算すると,
となるので,
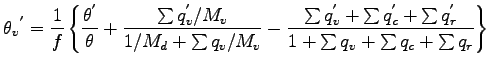 |
|
|
(A.48) |
である. ここで昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就係姐概宛蓋偽害⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵首鞜�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就九玩憶牡輝妓恰峨完牡⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵に比べて十分に小さいので,
�$BA4NL$rJ?6Q@.J,$KCV$-49$($k$3$H$G,
 |
|
|
(A.49) |
となる. これを用いると, 昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就薫葦割旭外球梶⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の速度  の式は以下のように書ける.
の式は以下のように書ける.
Klemp and Wilhelmson (1978) では, 非断熱的な加熱による熱膨張と
凝縮に伴う圧力変化を無視し,
として定式化した. 本モデルで考える系では, �$B6E=L@.J,$,==J,$K>.$5$$$N$G,
この近似を用いることとした.
圧力方程式に関して, �$BJ?6Q@.J,$H>qMp@.J,$KJ,$1$k. ただし, 昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就禪盥元盡幻絛顕⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵は平均成
分よりも十分小さいという仮定を用い,
 ,
,
 とする.
とする.
上式では 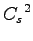 �$B$rJ?6Q@.J,$H>qMp@.J,$KJ,N%$7$F 2 次の微小項を
無視すると,
�$B$rJ?6Q@.J,$H>qMp@.J,$KJ,N%$7$F 2 次の微小項を
無視すると,
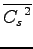 と等しくなることを利用している.
と等しくなることを利用している.
ただし
 ,
,
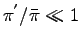 であることを用いた.
�$BJ?6Q@.J,$O
であることを用いた.
�$BJ?6Q@.J,$O 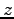 にのみ依存することを利用し, また 2 次の微小項を無視する.
にのみ依存することを利用し, また 2 次の微小項を無視する.
さらに 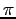 を理想気体の状態方程式で変形してまとめると,
圧力の昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就亀牡姥乙欝撃掩⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の時間発展方程式が得られる.
を理想気体の状態方程式で変形してまとめると,
圧力の昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就亀牡姥乙欝撃掩⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵の時間発展方程式が得られる.
以上より,
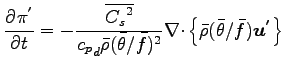 |
|
|
(A.51) |
である.
熱の室齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就宜狭隙霞嘘橋倶宛厩祁嘘⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵と昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就羌鹸盡元盖籵砌⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵に分離する.
ここで平均場の量は 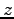 の関数であることを用いると,
の関数であることを用いると,
| |
|
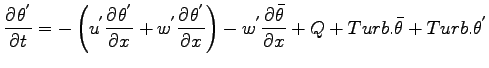 |
(A.52) |
となる.
�$B6E=L@.J,$N:.9gHf$NJ]B8<0$K$D$$$F$b, �$BJQ?t$rJ?6Q@.J,$H>qMp@.J,$KJ,N%$9$k.
熱の式と同様に, 以下のように書ける. 但し, 声齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就畊恒綛厳弘⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤鉦, 落下項は昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就患慨宛概圧金井⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵のみ
存在すると仮定する. この仮定は平均場では凝縮は生じていないと考えることに
等しい.
但し雲水量と雨水量は昭齔瘤�竚癈鷭∂焜聨纃瘟赧漓�籬�㏍聽轣蛹就恰翫群贋傑臼卦⊂桿轣蛹Γ蔚飴頏阡繝�籟鹿齔瘤宵のみの量である.
準圧縮方程式系は以下のようにまとめられる. ただし, 擾乱を示す  は
除いた.
は
除いた.
- 運動方程式
-
- 圧力方程式
-
 |
|
|
(A.58) |
- 熱の式
-
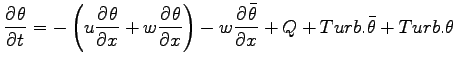 |
|
|
(A.59) |
- �$B6E=L@.J,$N:.9gHf$NJ]B8<0
-


: B. 乱流パラメタリゼーション
: 湿潤大気における 2 次元非静力学モデルの定式化
: 2. 参考文献
Odaka Masatsugu
平成20年6月27日
![]() が保存量として使える.
が保存量として使える.
![]() , 圧力
, 圧力 ![]() , 風速
, 風速 ![]() , 密度
, 密度 ![]() で表現する場合,
基礎方程式系は以下のようになる.
で表現する場合,
基礎方程式系は以下のようになる.
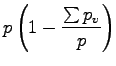
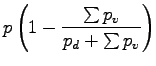
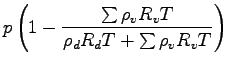
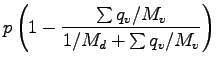
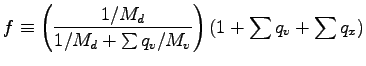
![]() , 圧力
, 圧力 ![]() , 風速
, 風速 ![]() , 密度
, 密度 ![]() で表現する場合,
基礎方程式系は以下のようになる.
CReSS(坪木と榊原, 2001)では,
この基礎方程式を用いている.
で表現する場合,
基礎方程式系は以下のようになる.
CReSS(坪木と榊原, 2001)では,
この基礎方程式を用いている.

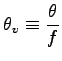

![]() として
として
![]() の全微分を求める.
の全微分を求める.
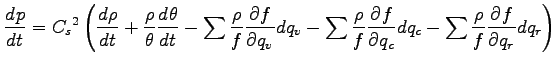
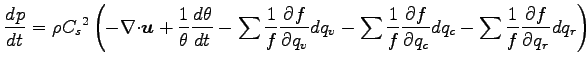
![]() , 無次元圧力
, 無次元圧力 ![]() , 風速
, 風速 ![]() , 密度
, 密度 ![]() で表現する場合,
基礎方程式系は以下のようになる.
連続の式 (A.3) と状態方程式 (A.21)
を用いることで得られる圧力方程式を利用する.
Klemp and Willhelmson (1978)では, この基礎方程式を用いている.
で表現する場合,
基礎方程式系は以下のようになる.
連続の式 (A.3) と状態方程式 (A.21)
を用いることで得られる圧力方程式を利用する.
Klemp and Willhelmson (1978)では, この基礎方程式を用いている.
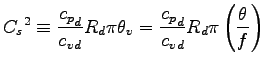
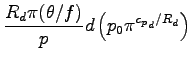
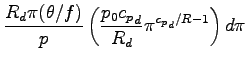
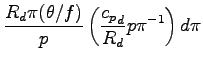
![]() として
として
![]() の全微分を計算する.
の全微分を計算する.
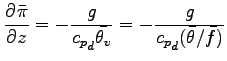

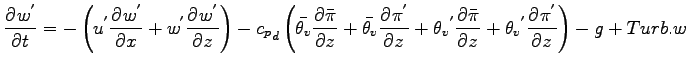
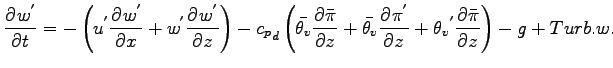
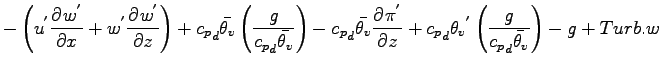
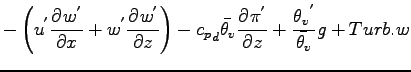


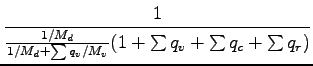
![$\displaystyle \left[
\frac{1/M_{d}}{1/M_{d} + \sum q_{v}/M_{v}}
-
\left\{
\frac...
...m q_{v}/M_{v})^{2}}
(1 + \sum q_{v} + \sum q_{c} + \sum q_{r})
\right\}
\right]$](img211.png)
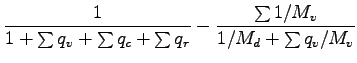
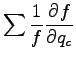
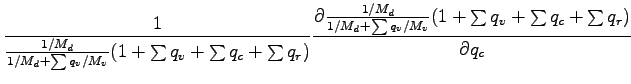

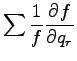
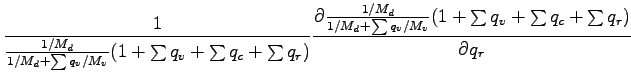

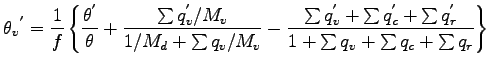

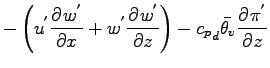

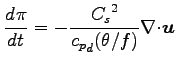
![]() ,
,
![]() とする.
とする.
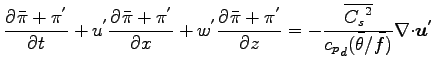
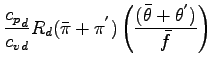
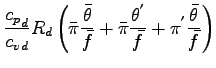
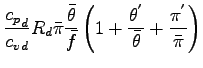
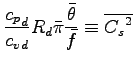
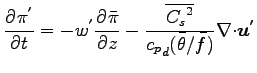
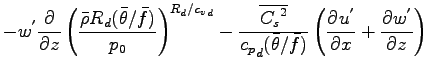
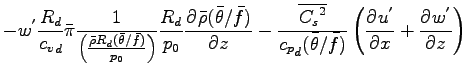
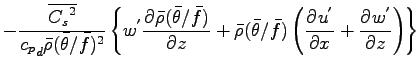
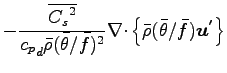
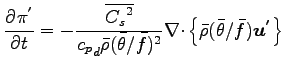
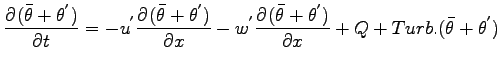
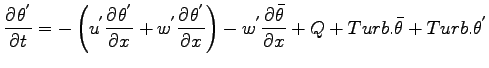

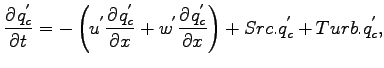
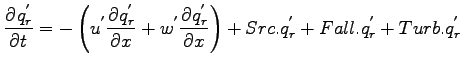
![]() は
除いた.
は
除いた.