スベルドラップ・バランス

(19) 式を海表面から海底まで鉛直に積分すると次のようになる.

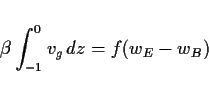$$\beta\int^0_{-1} v_g\,dz = f(w_E - w_B)$$ (36)

(31), (35) 式を (36) 式に代入すると

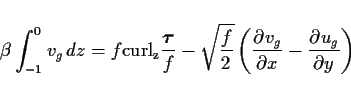$$\beta\int^0_{-1} v_g\,dz = f{\rm curl_z}\frac{\Dvect{\tau... ... - \sqrt{\frac{f}{2}} \left(\DP{v_g}{x} - \DP{u_g}{y}\right)$$ (37)

(37) 式左辺は地衡流量である. そこで, (29) 式の辺々を加 えて全質量輸送量を求めると,

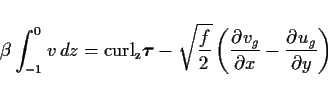$$\beta\int^0_{-1} v\,dz = {\rm curl_z}\Dvect{\tau} - \sqrt{\frac{f}{2}}\left(\DP{v_g}{x} - \DP{u_g}{y}\right)$$ (38)

となる. 特に (38) 式右辺第 2 項が他に比べて無視できるくらい小さ い場合には,

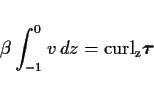$$\beta\int^0_{-1} v\,dz = {\rm curl_z}\Dvect{\tau}$$ (39)

となる. これを有次元で記述すると以下のようになる.

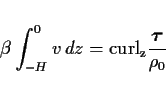$$\beta\int^0_{-H} v\,dz = {\rm curl_z}\frac{\Dvect{\tau}}{\rho_0}$$ (40)

これは南北質量輸送量と風応力との関係を表すもので, スベルドラップ・バラン スという. また右辺を 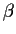$\beta$ で割り東西に積分したもの, すなわち風応力か ら推定される質量輸送量をスベルドラップ輸送量と呼ぶ. もし実際の海洋におい て(40) 式のバランスが成り立っていた場合には, この式によって海洋 の南北質量輸送量を風応力だけから推定することができる.

たとえば Hellerman and Rosenstein (1983)^[3]の年平均風応力デー タを用いて風応力の回転を求めると図 3 の ようになる. これを見ると, 北半球 の中緯度では負, 南半球の中緯度では正となっているのが分かる. (40) 式によれば, 両半球とも中緯度において赤道向きのスベルドラッ プ輸送量となる. 図 3 から流線関数場を求 めたものを図 4 に示す. ただしこれ は東岸における境界条件を 0 として西に向かって積分したものである. すなわ ち東岸境界層が存在しないことを仮定して求めたものである. これを見ると第 0 近似としては海洋大循環の力学的バランスが (40) 式で定性的に表さ れるように思える. それでは定量的にはどの程度 (40) 式のバランス が成り立っているのだろうか? これについて論じたものが, 小生が日本海洋学会 誌「海の研究」に投稿した総説「西岸境界流の流量は風応力から推定できるのか」 である.